Giải bài 143 tr 97 sách BT Toán lớp 8 Tập 1
Dựng hình thoi ABCD, biết cạnh bằng 2cm, một đường chéo bằng 3cm.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Dựng tam giác \(ABD\) có hai cạnh bằng \(2\,cm\) và cạnh đáy bằng độ dài đường chéo của hình thoi.
- Ở mặt phẳng đối diện, vẽ một tam giác chung cạnh đáy và độ dài cạnh bên bằng \(2\,cm.\)
- Chứng minh hình vừa dựng được thỏa mãn điều kiện bài toán.
Lời giải chi tiết
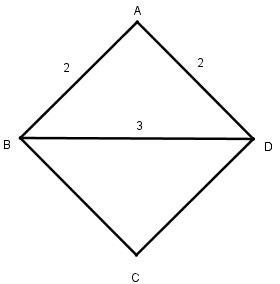
Cách dựng:
- Dựng \(∆ ABD\) biết \(AB = AD = 2\,(cm),\) \(BD = 3cm\)
- Trên nửa mặt phẳng bờ \(BD\) không chứa điểm \(A.\) Từ \(B\) dựng tia \(Bx // AD,\) từ \(D\) dựng tia \(Dy // AB,\) chúng cắt nhau tại \(C.\)
Ta có hình thoi \(ABCD\) cần dựng
Chứng minh:
Vì \(AB // CD\) và \(AD // BC\) nên tứ giác \(ABCD\) là hình bình hành
\(AB = AD = 2\,cm.\) Vậy tứ giác \(ABCD\) là hình thoi
Lại có: \(BD = 3\,cm\)
Hình thoi dựng được thỏa mãn điều kiện bài toán.
-- Mod Toán 8 HỌC247
-


Hi mọi người minh có bài muốn nhờ m.n giúp
bởi Chai Chai
 12/07/2018
12/07/2018
Cho hình thoi ABCD có góc A = 60 0 trên cạnh AD lấy điểm M trên cạnh DC lấy điểm N sao cho AM = DN, Tam giác BMN là tam giác gì ? Vì sao?
Bạ nào giải dduoc bai nay chi minh vs nhé, minh cảm ơn ạ
Theo dõi (0) 2 Trả lời -


Chứng minh hình thoi
bởi Mai Anh
 11/07/2018
11/07/2018
Giup minh bài này nhé
Cho tam giác ABC, AD là phân giác. Đường thẳng qua D song song với AC cắt AB ở E, đường thẳng qua D song song với AB cắt AC ở F. Chứng minh rằng tứ giác AEDF là hình thoi
Theo dõi (0) 2 Trả lời -


Toán hình 9
bởi Ah'ss Min'ss
 24/08/2017
24/08/2017
1.Cho hình thang ABCD vuông góc tại A và D. Hai đường chéo vuông góc với nhau tại O. Biết AB= 2 căn 13, OA=6. Tính diện tích hình thang ABCD.
2.Cho hình thoi ABCD. 2 đường chéo cắt nhau tại O. Khoảng cách từ O đến mỗi cạnh hình thoi là h. AC=m, BD=n. Chứng minh 1/m^2 + 1/n^2 = 1/4h^2
Theo dõi (0) 1 Trả lời





