Giải bài 135 tr 97 sách BT Toán lớp 8 Tập 1
Tứ giác ABCD có tọa độ các đỉnh như sau: A(0; 2), B( 3; 0), C(0; −2 ), D(−3; 0). Tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó ?
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Vận dụng kiến thức : Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
- Chu vi hình tứ giác bằng tổng độ dài các cạnh của hình đó.
Lời giải chi tiết
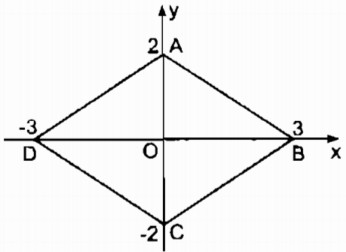
A(0; 2) và C(0; −2) nên hai điểm A và C đối xứng nhau qua O (0, 0) ⇒ OA = OC
B(3; 0) và D(−3; 0) nên hai điểm B và D đối xứng qua O (0; 0) ⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Ox ⊥ Oy hay AC ⊥ BD
Vậy tứ giác ABCD là hình thoi
Trong ∆ OAB vuông tại O. Theo định lý Pi-ta-go ta có:
\(\eqalign{ & A{B^2} = O{A^2} + O{B^2} \cr & A{B^2} = {2^2} + {3^2} = 4 + 9 = 13 \cr & AB = \sqrt {13} \cr} \)
Chu vi hình thoi bằng \(4\sqrt {13} \)
-- Mod Toán 8 HỌC247
-
Chứng minh giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi
bởi Đào Thị Nhàn
31/05/2019
Chứng minh rằng:
a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.
b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi
Theo dõi (0) 1 Trả lời -
Chứng minh AHCD là hình chữ nhật biết tam giác ABC cân tại A, AB=10cm, BC=12cm, đường cao AH
bởi bach hao
31/05/2019
ΔABC cân tại A, AB=10cm, BC=12cm, đường cao AH. Gọi M là trung điểm AC, D là điểm đói xứng của H qua M. Chứng minh
a) AHCD là hình chữ nhật
b) ABHD là hình bình hànhTheo dõi (0) 1 Trả lời -
Cho hình thoi ABCD, góc A= 60°, trên các cạnh AB, BC lấy điểm M, N sao cho BM+BN=AB.
CMR: đường trung trực của MN luôn đi qua một điểm cố định
Giúp mik vs nhé
mai mik học rTheo dõi (0) 1 Trả lời -
Chứng minh tứ giác ABEC là hình thoi biết hình bình hành ABCD có AB=AC
bởi Nguyễn Thủy
31/05/2019
Cho hình bình hành ABCD có AB=AC . Gọi M là trung điểm BC . Trên tia đối tia MA lấy ME=MA . CM : tứ giác ABEC là hình thoi .
D,C,E thẳng hàng
Theo dõi (0) 1 Trả lời -
Tứ giác AbCD có AB = CD. Gọi M, N theo thứ tự là trung điểm của BC , AD. Gọi I , K theo thứ tự là trung điểm của AC , BD. Chứng minh rằng MN là phân giác của góc IMK
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 133 trang 96 SBT Toán 8 Tập 1
Bài tập 134 trang 97 SBT Toán 8 Tập 1
Bài tập 136 trang 97 SBT Toán 8 Tập 1
Bài tập 137 trang 97 SBT Toán 8 Tập 1
Bài tập 138 trang 97 SBT Toán 8 Tập 1
Bài tập 139 trang 97 SBT Toán 8 Tập 1
Bài tập 140 trang 97 SBT Toán 8 Tập 1
Bài tập 141 trang 97 SBT Toán 8 Tập 1
Bài tập 142 trang 97 SBT Toán 8 Tập 1
Bài tập 143 trang 97 SBT Toán 8 Tập 1
Bài tập 11.1 trang 97 SBT Toán 8 Tập 1
