Giải bài 133 tr 96 sách BT Toán lớp 8 Tập 1
Chứng minh rằng trung điểm các cạnh của một hình thoi là đỉnh của một hình chữ nhật.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Vận dụng kiến thức : Hình bình hành có một góc vuông là hình chữ nhật.
Tính chất đường trung bình: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết
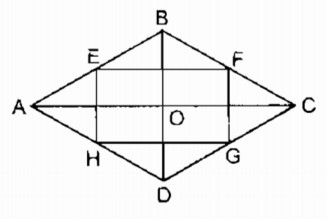
Giả sử hình thoi ABCD. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
- Trong ∆ ABC ta có:
E là trung điểm của AB
F là trung điểm của BC
nên EF là đường trung bình của tam giác ABC.
⇒ EF // AC và EF = \({1 \over 2}\)AC (tính chất đường trung bình của tam giác) (1)
- Trong ∆ ADC ta có:
H là trung điểm của AD
G là trung điểm của CD
nên HG là đường trung bình của ∆ ADC
⇒ HG // AC và HG = \({1 \over 2}\)AC ( tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Mặt khác: AC ⊥ BD (tính chất hình thoi)
EF // AC (chứng minh trên)
Suy ra: EF ⊥ BD
Trong ∆ ABD ta có EH là đường trung bình
⇒ EH // BD (tính chất đường trung bình của tam giác)
Suy ra: EH ⊥ EF hay = 1v
Vậy hình bình hành EFGH là hình chữ nhật.
-- Mod Toán 8 HỌC247
-


Cho tam giác ABC có BC= 7cm. Lấy E, F lầ lượt là trung điểm của AB và AC. Tính độ dài EF?
bởi Hoàng Trang
 29/11/2019
Cho tam giác ABC có BC= 7cm. Lấy E, F lầ lượt là trung điểm của AB và AC. Tính độ dài EF?Theo dõi (0) 4 Trả lời
29/11/2019
Cho tam giác ABC có BC= 7cm. Lấy E, F lầ lượt là trung điểm của AB và AC. Tính độ dài EF?Theo dõi (0) 4 Trả lời -


Cho hình thoi ABCD, gọi O là giao điểm 2 đường chéo, vẽ đường thẳng đi qua B và song song vs AC, vẽ đường thẳng đi qua C và song song với B
bởi Hoàng Trang
 29/11/2019
Cho hình thoi ABCD, gọi O là giao điểm 2 đường chéo, vẽ đường thẳng đi qua B và song song vs AC, vẽ đường thẳng đi qua C và song song với B. 2 đường chéo đó cắt nhau tại K.a, Tứ giác OBKC là hình j? Vì sao.b, Chứng minh rằng AB=OK.c, Tìm điều kiện của hình thoi ABCD để tứ giác OBKC là hình vuôngGIÚP MK VS SẮP THI RỒITheo dõi (0) 5 Trả lời
29/11/2019
Cho hình thoi ABCD, gọi O là giao điểm 2 đường chéo, vẽ đường thẳng đi qua B và song song vs AC, vẽ đường thẳng đi qua C và song song với B. 2 đường chéo đó cắt nhau tại K.a, Tứ giác OBKC là hình j? Vì sao.b, Chứng minh rằng AB=OK.c, Tìm điều kiện của hình thoi ABCD để tứ giác OBKC là hình vuôngGIÚP MK VS SẮP THI RỒITheo dõi (0) 5 Trả lời -

 Cho hình bình hành ABCD gọi K, I lần lượt là trung điểm AB , CDa) Tứ giác AKIC là hình gì ?b) Gọi E , F là giao Cho điểm của AI , KC với BD . Chứng minh BF = EF = EDc) Cần thêm điều kiện gì để AKIC là hình thoiTheo dõi (0) 1 Trả lời
Cho hình bình hành ABCD gọi K, I lần lượt là trung điểm AB , CDa) Tứ giác AKIC là hình gì ?b) Gọi E , F là giao Cho điểm của AI , KC với BD . Chứng minh BF = EF = EDc) Cần thêm điều kiện gì để AKIC là hình thoiTheo dõi (0) 1 Trả lời -

 Câu1: cho tam giác ABC, gọi E,F,D lần lượt là trung điểm của AB,AC,BC. a)Tính độ dài đoạn thẳng EF,biết BC=10cm b)chứng minh tứ giác BEFD là hình bình hành Câu2:cho tam giác ABC(góc A=90 độ) AM là trung tuyến.Biết AB=3cm, AC=4cm. a)tính độ dài cạnh AM b)gọi D là điểm đối xứng với A qua M.Tứ giác ABDC là hình gì? vì sao? c)Gọi E là điểm đối xứng với M qua AC.Chứng minh tứ giác AMCE là hình thoi GIÚP MÌNH LM 2 BÀI VS ẠTheo dõi (1) 4 Trả lời
Câu1: cho tam giác ABC, gọi E,F,D lần lượt là trung điểm của AB,AC,BC. a)Tính độ dài đoạn thẳng EF,biết BC=10cm b)chứng minh tứ giác BEFD là hình bình hành Câu2:cho tam giác ABC(góc A=90 độ) AM là trung tuyến.Biết AB=3cm, AC=4cm. a)tính độ dài cạnh AM b)gọi D là điểm đối xứng với A qua M.Tứ giác ABDC là hình gì? vì sao? c)Gọi E là điểm đối xứng với M qua AC.Chứng minh tứ giác AMCE là hình thoi GIÚP MÌNH LM 2 BÀI VS ẠTheo dõi (1) 4 Trả lời -


Cho tam giác ABC nhọn, có M, N là trung điểm của AB, BC. Tính độ dài của MN biết AC=9cm
bởi Quỳnh Nguyễn
 17/11/2019
17/11/2019
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời
Bài tập SGK khác
Bài tập 78 trang 106 SGK Toán 8 Tập 1
Bài tập 132 trang 96 SBT Toán 8 Tập 1
Bài tập 134 trang 97 SBT Toán 8 Tập 1
Bài tập 135 trang 97 SBT Toán 8 Tập 1
Bài tập 136 trang 97 SBT Toán 8 Tập 1
Bài tập 137 trang 97 SBT Toán 8 Tập 1
Bài tập 138 trang 97 SBT Toán 8 Tập 1
Bài tập 139 trang 97 SBT Toán 8 Tập 1
Bài tập 140 trang 97 SBT Toán 8 Tập 1
Bài tập 141 trang 97 SBT Toán 8 Tập 1
Bài tập 142 trang 97 SBT Toán 8 Tập 1
Bài tập 143 trang 97 SBT Toán 8 Tập 1
Bài tập 11.1 trang 97 SBT Toán 8 Tập 1





