Giải bài 4 tr 100 sách BT Toán lớp 7 Tập 1
a) Vẽ đường tròn tâm \(O\) bán kính \(2\,cm.\)
b) Vẽ góc \(AOB\) có số đo bằng \(60^\circ \). Hai điểm \(A, B\) nằm trên đường tròn \((O; 2cm)\).
c) Vẽ góc \(BOC\) có số đo bằng \(60^\circ \). Điểm \(C\) thuộc đường tròn \((O; 2cm).\)
d) Vẽ các tia \(OA’, OB’, OC’\) lần lượt là tia đối của các tia \(OA, OB, OC.\) Các điểm \(A’; B’; C’\) thuộc đường tròn \((O; 2cm).\)
e) Viết tên năm cặp góc đối đỉnh.
g) Viết tên năm cặp góc bằng nhau mà không đối đỉnh.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
- Tính chất: Hai góc đối đỉnh thì bằng nhau.
- Tổng hai góc kề bù bằng \(180^o\).
Lời giải chi tiết
a, b, c, d. Hình vẽ:
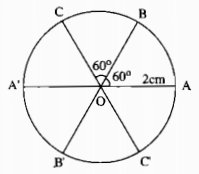
e) Tên 5 cặp góc đối đỉnh:
\(\widehat {AOB}\) và \(\widehat {A'OB'}\); \(\widehat {BOC}\) và \(\widehat {B'OC'}\);
\(\widehat {AOC}\) và \(\widehat {A'OC'}\); \(\widehat {AOB'}\) và \(\widehat {BOA'}\);
\(\widehat {AOC'}\) và \(\widehat {A'OC}\)
g) Vì \(\widehat {AOB} + \widehat {BOC} + \widehat {COA} = 180^\circ \) (Kề bù)
\( \Rightarrow \widehat {COA'} = 180^\circ - 60^\circ - 60^\circ = 60^\circ \)
Tên 5 cặp góc bằng nhau không đối đỉnh:
\(\eqalign{
& \widehat {AOB} = \widehat {BOC} = 60^\circ ;\widehat {BOC} + \widehat {COA'} = 60^\circ \cr
& \widehat {AOB} = \widehat {COA'} = 60^\circ ;\widehat {A'OB'} = \widehat {B'OC'} = 60^\circ \cr
& \widehat {AO{\rm{A}}'} = \widehat {BOB'} = 180^\circ \cr} \)
-- Mod Toán 7 HỌC247
-


Tính số đo các góc O1, O2 biết O1+O3=110 độ
bởi Nguyễn Quang Thanh Tú
 06/04/2019
06/04/2019
Cho hai đường thẳng cắt nhau tại điểm O như hình vẽ (1).
a/Kể tên các cặp góc đối đỉnh trong hình vẽ bên (không kể tên góc bẹt)
b/Biết rằng \(\widehat{O_1}+\widehat{O_3}=110^o\).Hãy tính số đo các góc : \(\widehat{O_1};\widehat{O_2}\)
Theo dõi (0) 1 Trả lời -


Bài 1:
Vẽ các cặp góc đối đỉnh A1 và A3 ;A2 và A4 được tạo ra khi hai đường thẳng cắt nhau tại A. Tìm số đo của mỗi góc trong những trường hợp sau
a) góc A1 bằng hai góc A2
b) góc A2 + góc A4=2200
c)A2-A1 =300
CÁC BẠN LÀM GIÚP MK VỚI, PLEASE. AI NHANH MK TICK CHO NHA
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh góc IBC=góc HAC biết tam giác ABC nhọn, AH vuông góc BC, BI vuông AC
bởi Van Tho
 06/04/2019
06/04/2019
Cho ΔABC nhọn. Vẽ AH vuông góc BC, BI vuông góc AC. Chứng minh \(\widehat{IBC}=\widehat{HAC}\)
Theo dõi (0) 1 Trả lời -


Tính số đo các góc BOE, AOE biết 2 đường thẳng AB và CD cắt tại O và góc AOC=30 độ
bởi Nguyễn Thị Trang
 06/04/2019
06/04/2019
cho 2 đường thẳng AB và CD cắt tại O. Trên nửa mặt phẳng bờ OD không chứa điểm B, kẻ Oe sao cho Od là tia phân giác của góc BOe. a, CM góc AOC = DOe b, Biết góc AOC = 30 độ. Tính số đo các góc BOe, AOe
Theo dõi (0) 1 Trả lời -


Hai góc đối đỉnh thì bằng nhau?
bởi thuy tien
 30/01/2019
30/01/2019
Các bn giúp mk làm câu này nhé:
Trong các câu sau, em hãy chọn câu sai:
1. Hai góc đối đỉnh thì bằng nhau
2. Hai góc bằng nhau thì đối đỉnh
3. Hai góc đối đỉnh thì có chung đỉnh
4. Góc đối đỉnh của góc vuông là góc vuông
5. Góc đối đỉnh của góc bẹt là chính góc bẹt đó
Theo dõi (0) 1 Trả lời -


cho 3 đường thẳng cắt nhau tại o
trong hình vẽ có tất cả bn góc
trong các góc ns trên có bn cặp tia đối đỉnh
Theo dõi (0) 1 Trả lời -


Cho góc xOy bằng 70 độ. Vẽ góc xOa và bOy kề bù với góc xOy.
a, tính góc xOa và bOy.
b, chứng tỏ rằng: góc xOa và góc bOy là hai góc đối đỉnh.
c, Om là tia phân giác của góc xOa.
On là tia phân giác của góc bOy.
Chứng tỏ rằng: Om và On là 2 tia đối nhau.
Theo dõi (0) 1 Trả lời -


Viết tên các cặp góc đối đỉnh biết 2 đường thẳng AB và CD cắt nhau tại O và BOC=120 độ
bởi hi hi
 30/01/2019
30/01/2019
cho 2 đường thẳng AB và CD
Cắt nhau tại O tạo thành BOC=120
a, Viết tên các cặp góc đối đỉnh(khác góc bẹt)
b, Tính số đo AOC,BOD,AOD
Theo dõi (0) 1 Trả lời -


Tính số đo các góc A3 và A4 biết 2 đường thẳng a và b cắt nhau tại A và A4=2A1
bởi Nguyễn Thị Thu Huệ
 30/01/2019
30/01/2019
cho 2 đường thẳng a và b
Cắt nhau tại A tạo thành các cặp góc đối đỉnh A1 và A3,A2 và A4
Tính số đo của A3 và A4 trong trường hợp sau
A4=2A1
Theo dõi (0) 1 Trả lời -


Tính số đo góc xOz biết góc xOy=80 độ, góc x'Oy' là góc đối đỉnh của góc xOy.
bởi Hong Van
 08/04/2019
08/04/2019
Cho góc xOy = 80 độ. Biết góc x'Oy' là góc đối đỉnh của góc xOy. Oz là tia phân giác của góc yOx'. Hãy vẽ hình minh họa và tính số đo góc xOz ?
Theo dõi (0) 1 Trả lời -


Viết tên các cặp góc đối đỉnh khi 2 đường thẳng aa' và bb' cắt nhau tại B
bởi Lê Nguyễn Hạ Anh
 08/04/2019
08/04/2019
Vẽ hai đường thẳng aa, và bb, cắt nhau tại A. Hãy viết tên các cặp góc đối đỉnh
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 99 SBT Toán 7 Tập 1
Bài tập 3 trang 100 SBT Toán 7 Tập 1
Bài tập 5 trang 100 SBT Toán 7 Tập 1
Bài tập 6 trang 100 SBT Toán 7 Tập 1
Bài tập 7 trang 100 SBT Toán 7 Tập 1
Bài tập 1.1 trang 100 SBT Toán 7 Tập 1
Bài tập 1.2 trang 101 SBT Toán 7 Tập 1





