Giải bài 30 tr 41 sách BT Toán lớp 7 Tập 2
Cho tam giác \(ABC.\) Gọi \(M\) là trung điểm của \(BC.\)
Chứng minh rằng \(\displaystyle AM < {{AB + AC} \over 2}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng tính chất hai tam giác bằng nhau
Sử dụng: Trong một tam giác:
+) Hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại
+) Độ dài một cạnh bao giờ cũng nhỏ hơn tổng độ dài của hai cạnh còn lại
Lời giải chi tiết
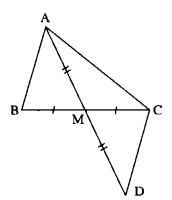
Trên tia đối của tia \(MA\) lấy điểm \(D\) sao cho \(MA = MD\)
* Xét \(∆AMB\) và \(∆DMC:\)
+) \(MA = MD \) (theo cách vẽ)
+) \(\widehat {AMB} = \widehat {DMC}\) (đối đỉnh)
+) \(MB = MC\) (gt)
Do đó: \(∆AMB = ∆DMC\) (c.g.c)
\( \Rightarrow AB = DC\) (hai cạnh tương ứng)
* Trong \(∆ACD\) ta có:
\(AD < AC + CD\) (bất đẳng thức tam giác)
Mà \(AD = AM + MD = 2AM\) và \(CD = AB\)
Nên \(AD < AC + CD\) \(\Rightarrow 2{\rm{A}}M < AC + AB\)\( \Rightarrow AM <\displaystyle {{AB + AC} \over 2}\)
-- Mod Toán 7 HỌC247
-
Giúp em nhanh với mấy anh chị ơi
Cho tam giác ABC, AC > AB. Gọi BE và CD là các trung tuyến. Chứng minh CD > BE.
Theo dõi (0) 2 Trả lời -
Cho tam giác ABC, trên tia CA lấy điểm D sao cho CD = CA, DT cắt cạnh AB tại E, cmr EA = EB
bởi thanh hằng
28/03/2018
Khó quá, mọi người giúp vs
Cho \(\Delta ABC\). Trên cạnh BC lây điểm T sao cho \(TB = \frac{2}{3}BC\).
Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Đườns thẳng DT cắt cạnh AB tại E. Chứng minh EA = EB.
Theo dõi (0) 2 Trả lời -
Kéo dài trung tuyến AM của tgiac ABC, G là trọng tâm, so sánh các cạnh của tgiac BGD
bởi thi trang
27/03/2018
Người ơi, giải giúp em vs, bài này khó quá!
Kéo dài trung tuyến AM của \(\Delta ABC\) một đoạn thẳng MD có độ dài bằng \(\frac{1}{3}\) độ dài AM. Gọi G là trọng tâm của \(\Delta ABC\). So sánh các cạnh của \(\Delta BGD\) với các trung tuyến của \(\Delta ABC\).
Theo dõi (0) 2 Trả lời -
ai giải hộ e bài này vs ạ
Cho \(\Delta \)ABC có BM, CN là hai đường trung tuyến cắt nhau tại G. Kéo dài BM lấy đoạn ME = MG. Kéo dài CN lấy đoạn NF = NG. Chứng minh:
- EF = BC.
- Đường thẳng AG di qua trung điểm BC.
Theo dõi (0) 2 Trả lời -
Cho hai đt x’x và y’y cắt nhau ở O, Ox lấy hai điểm A, B sao cho A nằm giữa O và B, AB = 20A
bởi ngọc trang
27/03/2018
Bài này khó quá giải giúp em vs
Cho hai đường thẳng x’x và y’y cắt nhau ở O. Trên tia Ox lấy hai điểm A và B sao cho A nằm giữa O và B, AB = 20A. Trên y’y lấy 2 điểm L và M sao cho O là trung điểm của đoạn thẳng LM. Nối B với L, B với M và gọi P là trung điểm của đoạn thẳng MB, Q là trung điểm của đoạn thẳng LB. Chứng minh các đoạn thẳng LP và MQ đi qua A.
Theo dõi (0) 2 Trả lời -
Cho tam giác ABC, AB bằng 1/2 AC, cmr BC > AB
bởi thuy tien
27/03/2018
Giúp mình giải câu này với!!
Cho tam giác ABC có \(\widehat B > {90^0},AB = \frac{1}{2}AC\). Chứng minh rằng
a. BC > AB
b. \(\widehat A < 2C\)
Theo dõi (0) 2 Trả lời -
Cho tam giác ABC, lấy điểm E, K lần lượt trên tia AB, AC sao cho AE + AK = AB + AC, cmr BC < EK
bởi minh dương
27/03/2018
Giúp em với ạ
Cho tam giác ABC cân tại A. Lấy các điểm E và K lần lượt trên các tia AB, AC sao cho AE + AK = AB + AC (E, K không trùng A, B, C)
Chứng minh: BC < EK
Theo dõi (0) 2 Trả lời -
e giải vẫn không ra, giúp em vs!
Cho tam giác ABC có AC > AB, điểm E nằm trên tia phân giác AD. Chứng minh rằng: AC – AB > EC – EB
Theo dõi (0) 1 Trả lời -
Cho điểm M nằm trong tam giác ABC, cmr tổng MA + MB + MC lớn hơn nửa chu vi
bởi thu phương
27/03/2018
help me me!!!
Cho điểm M nằm trong tam giác ABC. Chứng minh rằng tổng MA + MB + MC lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tam giác ABC.
Theo dõi (0) 3 Trả lời -
Cho điểm D nằm trên cạnh BC của tam giác ABC
bởi hà trang
28/03/2018
Giúp em với ạ
Cho điểm D nằm trên cạnh BC của tam giác ABC. Chứng minh rằng: \(\frac{{AB + AC - BC}}{2} < AD < \frac{{AB + AC + BC}}{2}\)
Theo dõi (0) 2 Trả lời -
Cho tam giác ABC có AC > AB, nối A với trung điểm M của BC, ss hai đoạn thẳng AB và CE
bởi thu hảo
27/03/2018
e giải vẫn không ra, giúp em vs!
Cho tam giác ABC có AC > AB. Nối A với trung điểm M của BC. Trên tia AM lấy điểm E sao cho M là trung điểm của đoạn thẳng AE. Nối C với E.
a. So sánh hai đoạn thẳng AB và CE
b. Chứng minh \(\frac{{AC - AB}}{2} < AM < \frac{{AC + AB}}{2}\)
Theo dõi (0) 1 Trả lời -
Ai đó giúp em với
Cho tam giác ABC, M là một điểm tùy ý ở miền trong tam giác ABC. Chứng minh MB + MC < AB + AC
Theo dõi (0) 2 Trả lời -
Hãy tìm độ dài ba cạnh của một tam giác, biết cạnh thứ nhất dài gấp rưỡi cạnh thứ hai
bởi minh dương
27/03/2018
Em cảm ơn nhiều ạ
Hãy tìm độ dài ba cạnh của một tam giác, biết cạnh thứ nhất dài gấp rưỡi cạnh thứ hai, cạnh thứ hai dài gấp rưỡi cạnh thứ ba và nữa chu vi tam giác bằng 9,5cm.
Theo dõi (0) 2 Trả lời
