Giải bài 3.9 tr 103 SBT Hình học 12
Trong không gian Oxyz cho một vecto \(\vec a\) tùy ý khác vecto \(\vec 0\). Gọi \(\alpha ,\beta ,\gamma \) là ba góc tạo bởi ba vecto đơn vị \(\vec i,\vec j,\vec k\) trên ba trục Ox, Oy, Oz và vecto \(\vec a\). Chứng minh rằng: \({\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1\)
Hướng dẫn giải chi tiết
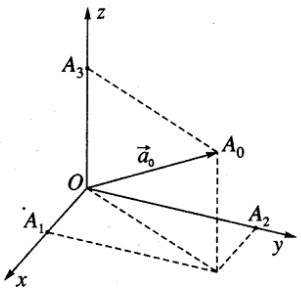
Gọi \(\overrightarrow {{a_0}} \) là vecto đơn vị cùng hướng với vecto \(\vec a\) , ta có \(\overrightarrow {{a_0}} = \frac{1}{{|\vec a|}}\vec a\)
Gọi \(\overrightarrow {O{A_0}} = \overrightarrow {{a_0}} \) và các điểm A1, A2, A3 theo thứ tự là hình chiếu vuông góc của điểm A0 trên các trục Ox, Oy, Oz.
Khi đó ta có: \(\frac{{|\overrightarrow {O{A_1}} |}}{{|\overrightarrow {O{A_0}} |}} = \cos \alpha ,\frac{{|\overrightarrow {O{A_2}} |}}{{|\overrightarrow {O{A_0}|} }} = \cos \beta ,\frac{{|\overrightarrow {O{A_3}} |}}{{|\overrightarrow {O{A_0}} |}} = \cos \gamma \)
Vì \(|\overrightarrow {O{A_0}} | = 1\) nên \(|\overrightarrow {O{A_1}} | = \cos \alpha ,|\overrightarrow {O{A_2}} | = \cos \beta ,|\overrightarrow {O{A_3}} | = \cos \gamma \)
Ta có \(\overrightarrow {O{A_0}} = \overrightarrow {O{A_1}} + \overrightarrow {O{B_2}} + \overrightarrow {O{A_3}} \) ta suy ra: \(\overrightarrow {O{A_0}} = \cos \alpha \vec i + \cos \beta \vec j + \cos \gamma \vec k\) hay \(\overrightarrow {O{A_0}} = (\cos \alpha ;\cos \beta ;\cos \gamma )\)
Vì \(\overrightarrow {O{A_0}} = \overrightarrow {{a_0}} \) mà \(\left| {\overrightarrow {{a_0}} } \right| = 1\) nên ta có: \({\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1\)
-- Mod Toán 12 HỌC247
-


Tìm khẳng định đúng?
bởi Le Thu Thao
 19/06/2020
19/06/2020
Chỉ câu 37
 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Viết phương trình mặt phẳng p đi qua hai điểm A( 0, -1 , 2) B ( 1 , 0, 3) và tiếp xúc với mặt cầu \((S) : ( x-1)^2 + ( y-2)^2 +( z+1)^2= 0\)?
bởi Thoa Ung
 10/06/2020
10/06/2020
Trong không gian với hệ toạ độ Oxyz, viết phương trình mặt phẳng p đi qua hai điểm A( 0, -1 , 2) B ( 1 , 0, 3) và tiếp xúc với mặt cầu \((S) : ( x-1)^2 + ( y-2)^2 +( z+1)^2= 0\)?
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính giá trị a + b + c?
bởi Lan Ngọc
 03/06/2020
03/06/2020
Cho mình hỏi câu 48 49 với mn ạ chỉ mình cách làm với
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Phương trình mặt cầu đường kính AB là?
bởi Hoa Lan Mai Huong
 02/06/2020
02/06/2020
1: Trong không gian với hệ toạ độ Oxyz cho A(1;3;5) , B(-5;-3;-1). Phương trình mặt cầu đường kính AB là?
2: Trong không gian với hệ toạ độ Oxyz, tìm tất cả các giá trị m để phương trình x² y² z² - 2x - 2y - 4z m= 0 là phương trình của một mặt cầu.
Theo dõi (0) 0 Trả lời -


Tìm tọa độ vectơ b?
bởi Huỳnh Dung
 24/05/2020
24/05/2020
a(1;-2;3). Tìm toạ độ vector b biết b ngược hướng a và độ dài b=2a
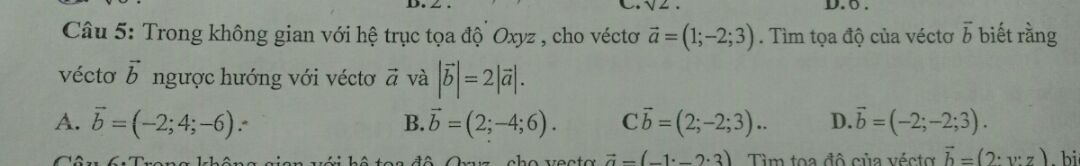 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x 2y 3z−6=0(P):x 2y 3z−6=0. Giao điểm của (P) với trục Oy là:
bởi Nguyễn Kim Ngọc
 22/05/2020
22/05/2020
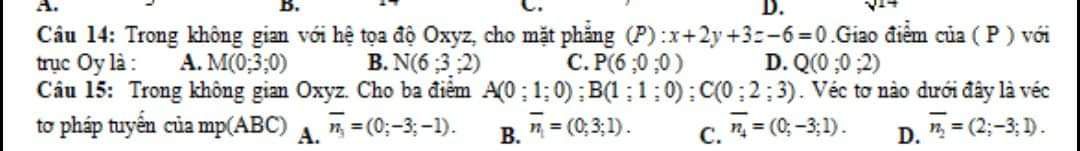 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm tọa độ điểm M để \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|\) nhỏ nhất ?
bởi Trang Thu
 16/05/2020
16/05/2020
Mn giải giúp mình câu 42 với ạ
 Theo dõi (2) 1 Trả lời
Theo dõi (2) 1 Trả lời -


Trong oxyz tính độ dài đường kính của mặt cầu?
bởi Thanh Huyền
 06/05/2020
06/05/2020
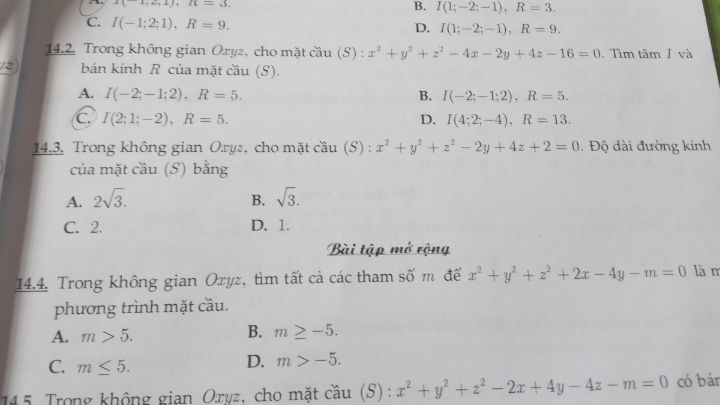 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3.7 trang 102 SBT Hình học 12
Bài tập 3.8 trang 102 SBT Hình học 12
Bài tập 3.10 trang 103 SBT Hình học 12
Bài tập 3.11 trang 103 SBT Hình học 12
Bài tập 3.12 trang 103 SBT Hình học 12
Bài tập 3.13 trang 103 SBT Hình học 12
Bài tập 3.14 trang 103 SBT Hình học 12
Bài tập 3.15 trang 103 SBT Hình học 12
Bài tập 3.16 trang 103 SBT Hình học 12
Bài tập 1 trang 81 SGK Hình học 12 NC
Bài tập 2 trang 81 SGK Hình học 12 NC
Bài tập 3 trang 81 SGK Hình học 12 NC
Bài tập 4 trang 81 SGK Hình học 12 NC
Bài tập 5 trang 81 SGK Hình học 12 NC
Bài tập 6 trang 81 SGK Hình học 12 NC
Bài tập 7 trang 81 SGK Hình học 12 NC
Bài tập 8 trang 81 SGK Hình học 12 NC
Bài tập 9 trang 81 SGK Hình học 12 NC
Bài tập 10 trang 81 SGK Hình học 12 NC
Bài tập 11 trang 81 SGK Hình học 12 NC
Bài tập 12 trang 82 SGK Hình học 12 NC





