Bài tập 12 trang 82 SGK Hình học 12 NC
Cho hình chóp S.ABC có đường cao SA = h, đáy là tam giác ABC vuông tại C, AC = b, BC = a. Gọi M là trung điểm của AC và N là điểm sao cho \(\overrightarrow {SN} = \frac{1}{3}\overrightarrow {SB} \)
a) Tính độ dài đoạn thẳng MN.
b) Tìm sự liên hệ giữa a, b, h để MN vuông góc với SB.
Hướng dẫn giải chi tiết
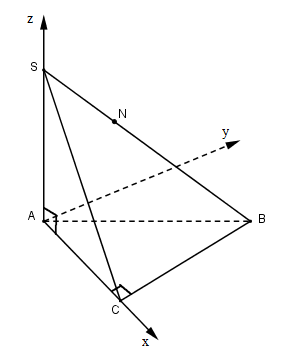
Chọn hệ trục Oxyz như hình vẽ, B nằm trong góc xOy.
Ta có: A = (0; 0; 0), C = (b; 0; 0), B = (b; a; 0), S = (0; 0; h).
\(M\left( {\frac{b}{2};0;0} \right),\overrightarrow {SB} = (b;a; - h)\)
Gọi N(x; y; z) thì \(\overrightarrow {SN} = \left( {x;y;z - h} \right)\)
\(\begin{array}{l}
\overrightarrow {SN} = \frac{1}{3}\overrightarrow {SB} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = \frac{b}{3}}\\
{y = \frac{a}{3}}\\
{z - h = \frac{{ - h}}{3}}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = \frac{b}{3}}\\
{y = \frac{a}{3}}\\
{z = \frac{{2h}}{3}}
\end{array}} \right. \Rightarrow N\left( {\frac{b}{3};\frac{a}{3};\frac{{2h}}{3}} \right)
\end{array}\)
a)
\(\begin{array}{*{20}{l}}
{\overrightarrow {MN} = \left( {\frac{b}{3} - \frac{b}{2};\frac{a}{3};\frac{{2h}}{3}} \right) = \left( { - \frac{b}{6};\frac{a}{3};\frac{{2h}}{3}} \right)}\\
\begin{array}{l}
MN = \sqrt {\frac{{{b^2}}}{{36}} + \frac{{{a^2}}}{9} + \frac{{4{h^2}}}{9}} \\
= \frac{1}{6}\sqrt {{b^2} + 4{a^2} + 16{h^2}}
\end{array}
\end{array}\)
b)
\(\begin{array}{l}
MN \bot SB \Leftrightarrow \overrightarrow {MN} .\overrightarrow {SB} = 0\\
\Leftrightarrow - \frac{{{b^2}}}{6} + \frac{{{a^2}}}{3} + \frac{{ - 2{h^2}}}{3} = 0\\
\Leftrightarrow 4{h^2} = 2{a^2} - {b^2}
\end{array}\)
-- Mod Toán 12 HỌC247
-


Viết phương trình mặt cầu đi qua hai điểm A, B và có tâm I nằm trên trục Oy
bởi Lê Gia Bảo
 07/02/2017
07/02/2017
Trong không gian với hệ tọa độ Oxyz cho A(-1; 2; 1); B(2; -2; 4); C(0; -4; 1). Chứng minh ba điểm A, B, C không thẳng hàng. Viết phương trình mặt cầu đi qua hai điểm A, B và có tâm I nằm trên trục Oy.
Theo dõi (0) 2 Trả lời -


Tìm tọa độ điểm I cách đều 4 điểm A, B, C, D
bởi thanh hằng
 07/02/2017
07/02/2017
Trong không gian tọa độ Oxyz cho 4 điểm A(1;0;0), B(0;-2;0), C(0;0;3), D(1;-2;3). Tìm tọa độ điểm I cách đều 4 điểm A, B, C, D.
Theo dõi (0) 1 Trả lời -


Viết phương trình mặt cầu đi qua 3 điểm A(1;2;-4), B(1;-3;1), C(2;2;3) và có tâm nằm trên mặt phẳng Oxy
bởi Dương Minh Tuấn
 07/02/2017
07/02/2017
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt cầu đi qua 3 điểm A(1;2;-4), B(1;-3;1), C(2;2;3) và có tâm nằm trên mặt phẳng Oxy.
Theo dõi (0) 2 Trả lời -


Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC. A', B', C' là các điểm sao cho ABA'C, BCB'A và CAC'B là hình bình hành.
bởi Đặng Ngọc Trâm
 08/02/2017
08/02/2017
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC. A', B', C' là các điểm sao cho ABA'C, BCB'A và CAC'B là hình bình hành. Biết \(H_{1}(0;-2),H_{2}(2;-1)\) và \(H_{3}(0;1)\) là trực tâm của các \(\triangle BCA',\triangle CAB',\triangle ABC'.\) Tìm tọa độ các đỉnh của \(\triangle ABC.\)
Theo dõi (0) 1 Trả lời





