Giải bài 4 tr 53 sách GK Toán Hình lớp 11
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi \({G_{A}}^{}\), \({G_{B}}^{}\), \({G_{C}, {G_{D}}^{}}^{}\) lần lượt là trọng tâm của tam giác BCD, CDA, ABD, ABC. Chứng minh rằng, \(A{G_{A}, B{G_{B}, C{G_{C}, D{G_{D}}^{}}^{}}^{}}^{}\) đồng quy.
Hướng dẫn giải chi tiết bài 4
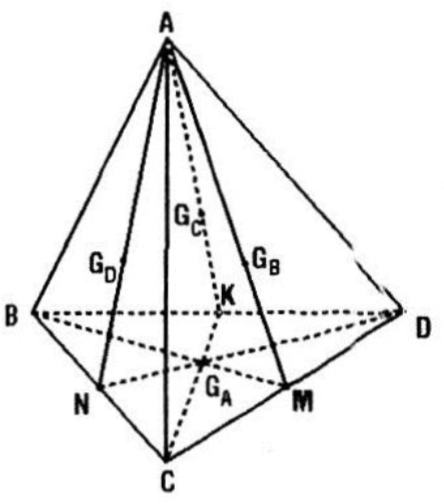
Gọi M, N, K lần lượt là trung điểm của CD, BC, BD.
Khi đó:
\(G_A\in BM\Rightarrow AG_A\subset (ABM)\)
\(G_B\in BM\Rightarrow AG_B\subset (ABM)\)
⇒ \(AG_A\) cắt \(AG_B\)
Tương tự: \(AG_A\subset (ACK); CG_C\subset (ACK)\)
⇒ \(AG_A\) cắt \(CG_C\) và \(BG_B\) cắt \(CG_C\) (Vì \(BG_C, CG_B\) cắt nhau tại trung điểm AD).
⇒ \(AG_A\), \(AG_B\), \(CG_C\) đồng quy (bài tập 3)
Hoàn toàn tương tự: \(BG_B, CG_C, DG_D\) đồng quy \(\Rightarrow AG_A, BG_B, CG_C, DG_D\) đồng quy.
-- Mod Toán 11 HỌC247
-
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Lấy điểm M thuộc cạnh SB sao cho MB = 2MS. Lấy điểm E thuộc cạnh SA và điểm F thuộc cạnh SC sao cho SE = 2AE và SF = 2FC. Mặt phẳng (MNE) cắt AD tại I và cắt CD tại K. a) Dựng điểm I và K và tìm thiết diện của hình chóp cắt bởi (MNE). b) Tính tỉ số IA / ID và KC / KD
bởi Nguyễn Hồng Dương
17/08/2021
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Lấy điểm M thuộc cạnh SB sao cho MB = 2MS. Lấy điểm E thuộc cạnh SA và điểm F thuộc cạnh SC sao cho SE = 2AE và SF = 2FC. Mặt phẳng (MNE) cắt AD tại I và cắt CD tại K. a) Dựng điểm I và K và tìm thiết diện của hình chóp cắt bởi (MNE). b) Tính tỉ số IA / ID và KC / KD
Theo dõi (0) 0 Trả lời -
Chóp SABCD có đáy không là hình thang. Xác định các giao tuyến sau: a) (SAC) giao (SBD) b) (SAB) giao (SCD) c) (SAD) giao (SBC)
bởi Bich Phuong
16/08/2021
Chóp SABCD có đáy không là hình thanga) (SAC) giao (SBD) b) (SAB) giao (SCD) c) (SAD) giao (SBC)Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 2 trang 53 SGK Hình học 11
Bài tập 3 trang 53 SGK Hình học 11
Bài tập 5 trang 53 SGK Hình học 11
Bài tập 6 trang 54 SGK Hình học 11
Bài tập 7 trang 54 SGK Hình học 11
Bài tập 8 trang 54 SGK Hình học 11
Bài tập 9 trang 54 SGK Hình học 11
Bài tập 10 trang 54 SGK Hình học 11
Bài tập 2.1 trang 63 SBT Hình học 11
Bài tập 2.2 trang 63 SBT Hình học 11
Bài tập 2.3 trang 63 SBT Hình học 11
Bài tập 2.4 trang 63 SBT Hình học 11
Bài tập 2.5 trang 64 SBT Hình học 11
Bài tập 2.6 trang 64 SBT Hình học 11
Bài tập 2.7 trang 64 SBT Hình học 11
Bài tập 2.8 trang 64 SBT Hình học 11
Bài tập 2.9 trang 64 SBT Hình học 11
Bài tập 1 trang 49 SGK Hình học 11 NC
Bài tập 2 trang 50 SGK Hình học 11 NC
Bài tập 3 trang 50 SGK Hình học 11 NC
Bài tập 4 trang 50 SGK Hình học 11 NC
Bài tập 5 trang 50 SGK Hình học 11 NC
Bài tập 6 trang 50 SGK Hình học 11 NC
Bài tập 7 trang 50 SGK Hình học 11 NC
Bài tập 8 trang 50 SGK Hình học 11 NC
Bài tập 9 trang 50 SGK Hình học 11 NC
Bài tập 10 trang 50 SGK Hình học 11 NC
Bài tập 11 trang 50 SGK Hình học 11 NC
Bài tập 12 trang 51 SGK Hình học 11 NC
Bài tập 13 trang 51 SGK Hình học 11 NC
Bài tập 14 trang 51 SGK Hình học 11 NC
