Bài tập 10 trang 50 SGK Hình học 11 NC
Cho hai đường thẳng a và b cắt nhau tại điểm O và đường thẳng c cắt mp(a , b) ở điểm I khác O. Gọi M là điểm di động trên c và khác I. Chứng minh rằng giao tuyến của các mặt phẳng (M , a), (M , b) nằm trên một mặt phẳng cố định
Hướng dẫn giải chi tiết
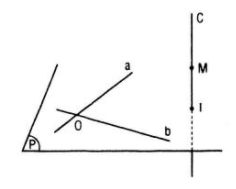
Ta có: M ∈ (M, a) ∩ (M, b)
Vì O = a ∩ b nên O ∈ (M, a) ∩ (M, b )
=> (M, a) ∩ (M, b) = MO
Vì M ∈ c nên MO ⊂ mp(O, c)
Vậy giao tuyến của hai mặt phẳng (M, a), (M, b) nằm trên mặt phẳng (O, c) cố định.
-- Mod Toán 11 HỌC247
Nếu bạn thấy
hướng dẫn giải
Bài tập 10 trang 50 SGK Hình học 11 NC HAY thì click chia sẻ
YOMEDIA
-
Tính diện tích thiết diện của tứ giác ABCD với mp(MEF)
bởi Thảo Thảo
15/10/2019
Theo dõi (0) 1 Trả lời -
Tìm giao tuyến của 2 mp (SAB) và (SCD) biết đáy (ABCD) có AB cắt CD tại E, AC cắt BD tại F
bởi Bảo An
14/10/2019
Bài 1
Theo dõi (0) 1 Trả lời
