Giải bài 10 tr 54 sách GK Toán Hình lớp 11
Cho hình chóp S. ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD
a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)
b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)
c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC)
d) Tìm giao điểm P của SC và mặt pẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM)
Hướng dẫn giải chi tiết bài 10
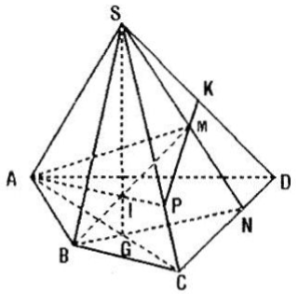
Câu a:
Trên mp(SCD) gọi N là giao điểm của SM và CD
⇒ N là giao điểm của CD và mp(SBM)
Câu b:
Gọi Q là giao điểm của BN và AC (trên mặt phẳng (ABCD))
⇒ S và Q là 2 điểm chung của 2 mặt phẳng (SBM) và (SAC).
\(\Rightarrow (SBM)\cap (SAC)=SQ\)
Câu c:
Gọi I là giao điểm của SQ và BM (trên mặt phẳng (SBM)).
Vì \(SQ\subset (SAC)\Rightarrow I\) là giao điểm của BM và mp(SAC)
Câu d:
Trên mặt phẳng (SAC) gọi P là giao điểm của AI và SC
Vì \(I\in BM, AI\subset (ABM)\Rightarrow P\) là giao điểm của SC và mp(ABM)
Trên mp(SCD) gọi K là giao điểm của SD và PM
Vì \(K\in PM\Rightarrow K\in (ABM)\)
⇒ 2 mặt phẳng (SCD) và (ABM) có 2 điểm chung P và K.
\(\Rightarrow (SCD)\cap (ABM)=PK\)
-- Mod Toán 11 HỌC247
-
Cho hình chóp O.ABC, A’ là trung điểm của OA; các điểm B’, C’ tương ứng thuộc các cạnh OB, OC và không phải là trung điểm của các cạnh này. Phát biểu nào sau đây là đúng.
bởi Choco Choco
21/01/2021
A. Giao tuyến của (OBC) và (A’B’C’) là A’B’;
B. Giao tuyến của (ABC) và (OC’A’) là CK, với K là giao điểm của C’B’ với CB
C. (ABC) và (A’B’C’) không cắt nhau
D. Giao tuyến của (ABC) và (A’B’C’) là MN, với M là giao điểm của AC và A’C’, N là giao điểm của BC và B’C’.
Theo dõi (0) 1 Trả lời -
Cho hình chóp S.ABCD, O là giao điểm của AC và BD, phát biểu nào sau đây là đúng?
bởi Đào Lê Hương Quỳnh
22/01/2021
A. Giao tuyến của (SAC) và (SBD) là SO.
B. Giao tuyến của (SAB) và (SCD) là điểm S.
C. Giao tuyến của (SBC) và (SCD) là SK, với K là giao điểm của SD và BC.
D. Giao tuyến của (SOC) và (SAD) là SM, với M là giao điểm của AC và SD.
Theo dõi (0) 1 Trả lời
