Giải bài 2.9 tr 64 SBT Hình học 11
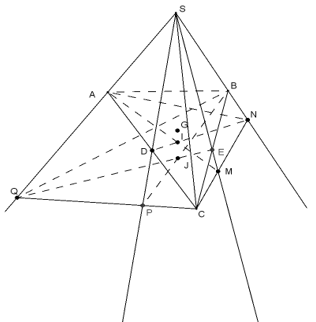
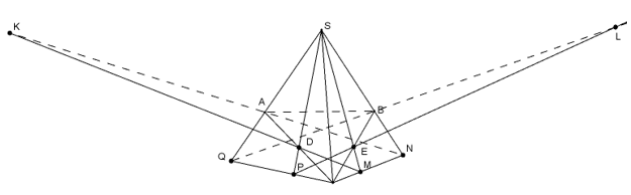
Cho tứ diện S.ABC có D, E lần lượt trung điểm AC, BC và G là trọng tâm tam giác ABC. Mặt phẳng (α) qua AC cắt SE, SB lần lượt tại M, N. Một mặt phẳng (β) qua BC cắt SD và SA lần lượt tại P và Q.
a) Gọi I = AM ∩ DN, J = BP ∩ EQ. Chứng minh bốn điểm S, I, J, G thẳng hàng.
b) Giả sử AN ∩ DM = K, BQ ∩ EP = L. Chứng minh ba điểm S, K, L thẳng hàng.
Hướng dẫn giải chi tiết
a) Ta thấy:
+ G là trọng tâm tam giác ABC ⇒ G ∈ BD ⇒ G ∈ BD
+ I ∈ DN (theo cách dựng hình).
+ J ∈ BP (theo cách dựng hình).
⇒ S, I, J, G ∈ mp(SPN)
Tương tự ⇒ S, I, J, G ∈ mp(SQM)
Vậy S, I, J, G là điểm chung của mp(SPN) và mp(SQM)
b)
Ta thấy:
+ S = PD ∩ EM
+ K ∈ DM
+ L ∈ PE
⇒ S, K, L ∈ (SPM)
Tương tự ⇒ S, K, L ∈ (SQN)
Vậy S, K, L là điểm chung của (SPM) và (SQN)
-- Mod Toán 11 HỌC247
-
Tìm giao tuyến của mặt phẳng (A'CD) với các mặt phẳng (SAB); (SBC); (SCD); (SDA)?
bởi Trần Đăng Phúc
13/08/2020
Cho hình chóp S.ABCD có AB và CD cắt nhau. Lấy A' là điểm nằm giữa S và A. Tìm giao tuyến của mặt phẳng (A'CD) với các mặt phẳng (SAB); (SBC); (SCD); (SDA)Theo dõi (0) 0 Trả lời -
Chứng minh SO vuông góc (ABCD)?
bởi Nguyễn Hoàng Nguyên
14/04/2020
Giúp e câu 5,6,7,8 vs ạ
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 2.7 trang 64 SBT Hình học 11
Bài tập 2.8 trang 64 SBT Hình học 11
Bài tập 1 trang 49 SGK Hình học 11 NC
Bài tập 2 trang 50 SGK Hình học 11 NC
Bài tập 3 trang 50 SGK Hình học 11 NC
Bài tập 4 trang 50 SGK Hình học 11 NC
Bài tập 5 trang 50 SGK Hình học 11 NC
Bài tập 6 trang 50 SGK Hình học 11 NC
Bài tập 7 trang 50 SGK Hình học 11 NC
Bài tập 8 trang 50 SGK Hình học 11 NC
Bài tập 9 trang 50 SGK Hình học 11 NC
Bài tập 10 trang 50 SGK Hình học 11 NC
Bài tập 11 trang 50 SGK Hình học 11 NC
Bài tập 12 trang 51 SGK Hình học 11 NC
Bài tập 13 trang 51 SGK Hình học 11 NC
Bài tập 14 trang 51 SGK Hình học 11 NC
