Bài tập 5 trang 50 SGK Hình học 11 NC
Cho mặt phẳng (P) và ba điểm không thẳng hàng A, B, C cùng nằm ngoài (P). Chứng minh rằng nếu ba đường thẳng AB, BC, CA đều cắt mp (P) thì các giao điểm đó thẳng hàng
Hướng dẫn giải chi tiết
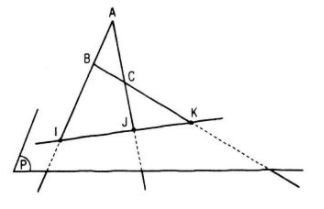
Gọi I, J, K lần lượt là giao điểm của AB, AC, BC với mp(P). A, B, C không thẳng hàng nên có mp(ABC).
Rõ ràng I, J, K ϵ mp(ABC) và I, J, K nằm trên giao tuyến của hai mặt phẳng (P) và (ABC).
Vậy I, J, K thẳng hàng.
-- Mod Toán 11 HỌC247
-
Tìm thiết diện của hình chóp cắt bởi mp (MNP) biết M,N là trung điểm của AB, CD
bởi Phạm Hòa Thuận
05/12/2019
Cho tứ diện ABCD. Gọi M,N là trung điểm của AB, CD. Gọi P là điểm thuộc AD sao cho P không trùng với trung điểm của AD.Tìm thiết diện của hình chóp cắt bởi mp (MNP)
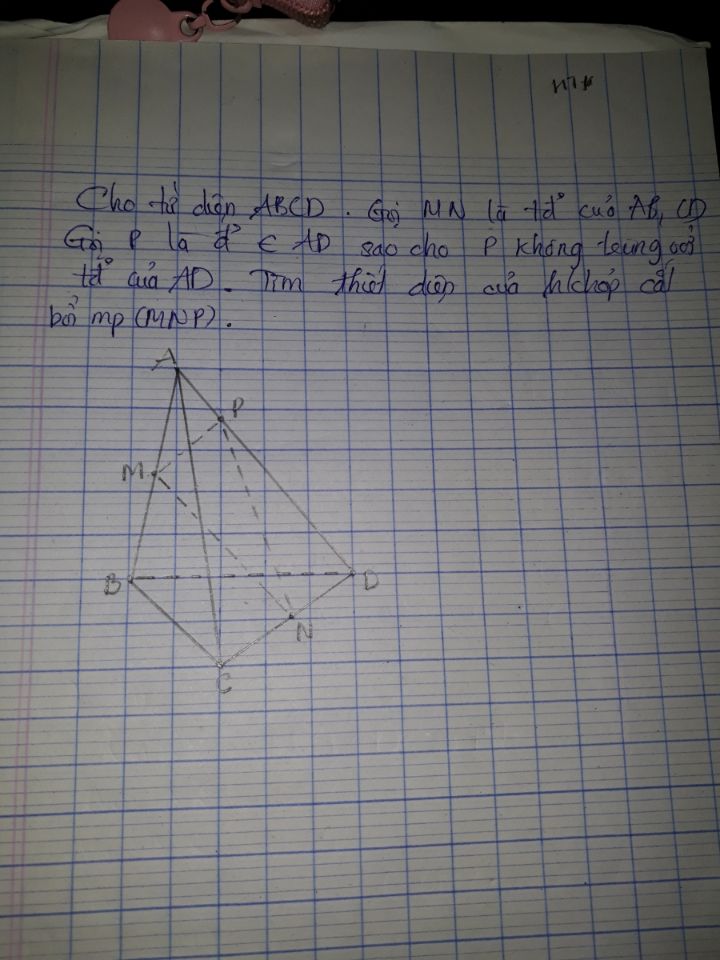Theo dõi (0) 0 Trả lời -
Tìm giao tuyến của (HIK) và (ABC) biết H, K là trọng tâm tam giác SAB, SCD
bởi Hán Thị Kim Dung
02/12/2019
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 3 trang 50 SGK Hình học 11 NC
Bài tập 4 trang 50 SGK Hình học 11 NC
Bài tập 6 trang 50 SGK Hình học 11 NC
Bài tập 7 trang 50 SGK Hình học 11 NC
Bài tập 8 trang 50 SGK Hình học 11 NC
Bài tập 9 trang 50 SGK Hình học 11 NC
Bài tập 10 trang 50 SGK Hình học 11 NC
Bài tập 11 trang 50 SGK Hình học 11 NC
Bài tập 12 trang 51 SGK Hình học 11 NC
Bài tập 13 trang 51 SGK Hình học 11 NC
Bài tập 14 trang 51 SGK Hình học 11 NC
