Bài tập 3 trang 53 SGK Hình học 11

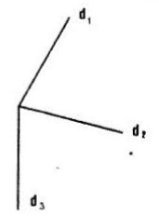
Giả sử \(d_1, d_2, d_3\) không đồng quy. Tức là: d₁ lần lượt cắt d₂ và d₃ tại A và B.

Gọi \(\alpha\) là mặt phẳng qua 2 đường thẳng cắt nhau d₂ và d₃. Khi đó: 

\(A\in (\alpha ), B\in (\alpha )\) và \(A\in d_1, B\in d_1\)

⇒ d1 nằm trong mặt phẳng \((\alpha )\)

⇒ \(d_1, d_2, d_3\) cùng nằm trên 1 mặt phẳng (trái với giả thiết)

⇒ \(d_1, d_2, d_3\) đồng quy.

-- Mod Toán 11 HỌC247