Bài tập 11 trang 50 SGK Hình học 11 NC
Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mp(P). Gọi M là điểm nằm giữa S và A ; N là điểm giữa S và B; giao điểm của hai đường thẳng AC và BD là O
a. Tìm giao điểm của mặt phẳng (CMN) với đường thẳng SO
b. Xác định giao tuyến của hai mặt phẳng (SAD) và (CMN)
Hướng dẫn giải chi tiết
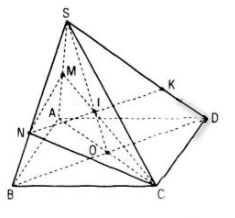
a) Tìm SO ∩ (CNM)
Trong mặt phẳng (SAC) gọi I là giao điểm của SO với CM
I = SO ∩ CM
mà CM ⊂ (CMN) nên I = SO ∩ (CMN)
b) Tìm (SAD) ∩ (CMN)
Trong mp(SBD) gọi K là giao điểm của NI và SD: K = NI ∩ SD
Ta có: M, K ∈ (CMN) và M, K ∈ (SAD)
Do đó (SAD) ∩ (CMN) = MK
-- Mod Toán 11 HỌC247
-


Hình chóp từ giác có bao nhiêu mặt ?
bởi Hoài Linh
 12/12/2018
12/12/2018
A.8
B.6
C.5
D.4Theo dõi (0) 7 Trả lời -


Cho tứ diện SABC. Lấy E, F trên SA và SB sao cho SA = 2 SE, SF = 2 FA. G là trọng tâm của tam giác ABC. Tìm giao tuyến của:
1. ( EFG ) và ( ABC )
2. ( EFG ) và ( SGC )
MÌNH CHỈ CẦN VẼ GIÙM MÌNH CÁI HÌNH THÔI ẠTheo dõi (0) 3 Trả lời





