Bài tập 2.8 trang 64 SBT Hình học 11

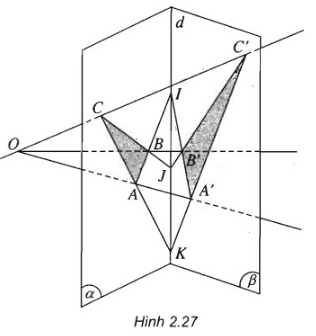
Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến d. Trong (α) lấy hai điểm A và B sao cho AB cắt d tại I. O là một điểm nằm ngoài (α) và (β) sao cho OA và OB lần lượt cắt (β) tại A’ và B’.

a) Chứng minh ba điểm I, A’, B’ thẳng hàng.

b) Trong (α) lấy điểm C sao cho A, B, C không thẳng hàng. Giả sử OC cắt (β) tại C’, BC cắt B’C’ tại J, CA cắt C’A’ tại K. Chứng minh I, J, K thẳng hàng.