Giải bài 2 tr 53 sách GK Toán Hình lớp 11
Gọi M là giao điểm của đường thẳng d và mặt phẳng \((\alpha )\). Chứng minh M là điểm chung của \((\alpha )\) với một mặt phẳng bất kì chứa d
Hướng dẫn giải chi tiết bài 2
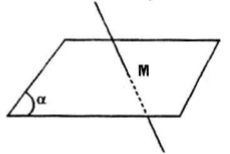
Gọi (\(\beta\)) là mặt phẳng bất kì chứa đường thẳng d.
Khi đó: \(M\in d\Rightarrow M\in (\beta )\) và \(M\in (\alpha )\)
⇒ M là điểm chung của \((\alpha )\) và \((\beta )\)
⇒ M là điểm chung của \((\alpha )\) với mọi mặt phẳng bất kỳ chứa d.
-- Mod Toán 11 HỌC247
-
Cho hình chóp S ABCD có đáy ABCD là hình bình hành. N là trung điểm của SB, M là một điểm nằm trên cạnh SC sao cho MC=2SM. Tìm giao điểm của SB, SD và (AMN)
bởi Hà Yên
30/11/2021
Cho hình chóp S ABCD có đáy ABCD là hình bình hành. N là trung điểm của SB, M là một điểm nằm trên cạnh SC sao cho MC=2SM:
a, Tìm giao điểm của SB, SD và (AMN)
b, Tìm E và AM giao (SBD)
c, Tìm P và SD giao (AMN)
d, Hãy tìm các đoạn giao tuyến của (AMN) với các mặt của hình chóp.
Theo dõi (0) 0 Trả lời -
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm. Gọi O, J, K, lần lượt là trung điểm của SB, CD,CB . Tìm giao tuyến của ( OJK) và (SAB)
bởi NTHNgoc
12/11/2021
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm. Gọi O, J, K, lần lượt là trung điểm của SB, CD,CB . Tìm giao tuyến của ( OJK) và (SAB) A. Đường thẳng qua O và qua giao điểm của JK và AD. B. Đường thẳng qua O và song song SA. C. Đường thẳng qua O và qua giao điểm ocủa JK và AB. D. Đường thẳng qua O và song song AB.Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1 trang 53 SGK Hình học 11
Bài tập 3 trang 53 SGK Hình học 11
Bài tập 4 trang 53 SGK Hình học 11
Bài tập 5 trang 53 SGK Hình học 11
Bài tập 6 trang 54 SGK Hình học 11
Bài tập 7 trang 54 SGK Hình học 11
Bài tập 8 trang 54 SGK Hình học 11
Bài tập 9 trang 54 SGK Hình học 11
Bài tập 10 trang 54 SGK Hình học 11
Bài tập 2.1 trang 63 SBT Hình học 11
Bài tập 2.2 trang 63 SBT Hình học 11
Bài tập 2.3 trang 63 SBT Hình học 11
Bài tập 2.4 trang 63 SBT Hình học 11
Bài tập 2.5 trang 64 SBT Hình học 11
Bài tập 2.6 trang 64 SBT Hình học 11
Bài tập 2.7 trang 64 SBT Hình học 11
Bài tập 2.8 trang 64 SBT Hình học 11
Bài tập 2.9 trang 64 SBT Hình học 11
Bài tập 1 trang 49 SGK Hình học 11 NC
Bài tập 2 trang 50 SGK Hình học 11 NC
Bài tập 3 trang 50 SGK Hình học 11 NC
Bài tập 4 trang 50 SGK Hình học 11 NC
Bài tập 5 trang 50 SGK Hình học 11 NC
Bài tập 6 trang 50 SGK Hình học 11 NC
Bài tập 7 trang 50 SGK Hình học 11 NC
Bài tập 8 trang 50 SGK Hình học 11 NC
Bài tập 9 trang 50 SGK Hình học 11 NC
Bài tập 10 trang 50 SGK Hình học 11 NC
Bài tập 11 trang 50 SGK Hình học 11 NC
Bài tập 12 trang 51 SGK Hình học 11 NC
Bài tập 13 trang 51 SGK Hình học 11 NC
Bài tập 14 trang 51 SGK Hình học 11 NC
