Ở bài 31, các em đã được tìm hiều về khái niệm đạo hàm và phương pháp tính đạo hàm bằng định nghĩa. Khuyết điểm của phương pháp này là rất khó áp dụng với các hàm số phức tạp, và phải trải qua nhiều công đoạn tính toán. Bài 32 Quy tắc tính đạo hàm trong chương trình Toán 11 Kết Nối Tri Thức sẽ giới thiệu đến các em công thức tính đạo hàm của các hàm số thường gặp và hàm hợp của chúng, các quy tắc tính đạo hàm của tổng, hiệu, tích, thương.
Tóm tắt lý thuyết
1.1. Đạo hàm của một số hàm số thường gặp
a) Đạo hàm của hàm số y = \(x^n\) (n \(\in\) N)
\[{\left( {{x^n}} \right)'} = n{x^{n - 1}}, x\in R.\]
b) Đạo hàm của hàm số y = \(\sqrt x\)
1.2. Đạo hàm của tổng, hiệu, tích, thương
Giả sử \(u = u\left( x \right)\) và \(v = v\left( x \right)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng (a; b). Ta có:
+ \({\left( {u + v} \right)'} = {u'} + {v'}\)
+ \({\left( {u - v} \right)'} = {u'} - {v'}\)
+ \({\left( {u.v} \right)'} = {u'}.v + u.{v'}\)
+ \(\left ( \frac{u}{v} \right )'=\frac{u'v-uv'}{v^2}, (v(x) \ne 0)\)
Chú ý:
- \({\left( {\frac{1}{v}} \right)'} = - \frac{{ - v'}}{{{v^2}}}\) , \((v(x)\ne 0)\)
1.3. Đạo hàm của hàm số hợp
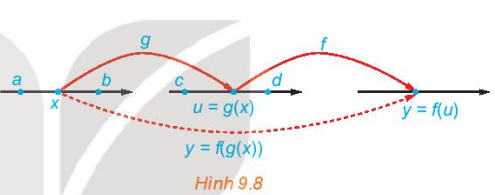
a) Khái niệm hàm số hợp
Giả sử u = g(x) là hàm số xác định trên khoảng (a; b), có tập giá trị chứa trong khoảng (c, d) và y = f(u) là hàm số xác định trên khoảng (c; d). Hàm số y = f(g(x)) được gọi là hàm số hợp của hàm số y = f(u) với u = g(x).
b) Đạo hàm của hàm số hợp
Nếu hàm số u = g(x) có đạo hàm \(u'_x\) tại x và hàm số y = f(u) có đạo hàm \(y'_u\) tại u thì hàm số hợp y = f(g(x)) có đạo hàm \(y'_x\) tại x là
1.4. Đạo hàm của hàm số lượng giác
a) Đạo hàm của hàm số y = sin x
Hàm số y = sinx có đạo hàm trên R và (sin x)' = cos x.
Đối với hàm số hợp y = sinu, với u = u(x), ta có (sinu)' = u'. cosu.
b) Đạo hàm của hàm số y = cos x
Hàm số y = cosx có đạo hàm trên R và ( cos x )' = - sin x.
Đối với hàm số hợp y = cosu, với u = u(x), ta có: (cosu)' =–u'. sinu.
c) Đạo hàm của các hàm số y= tan x và y = cot x
1.5. Đạo hàm của hàm số mũ và hàm số lôgarit
a) Giới hạn liên quan đến hàm số mũ và hàm số lôgarit
\(\begin{array}{l} \mathop {\lim }\limits_{x \to 0} {\left( {1 + x} \right)^{\frac{1}{x}}} = e;\\ \mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + x} \right)}}{x} = 1;\\ \mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - 1}}{x} = 1. \end{array}\)
b) Đạo hàm của hàm số mũ
\(\begin{array}{l} \left( {{e^x}} \right)' = {e^x}, \text{với mọi }x \in R \\ \Rightarrow \left( {{e^u}} \right)' = u'.{e^u}\\ \left( {{a^x}} \right)' = {a^x}\ln a,\,\text{với mọi }0 < a \ne 1,\,x \in R \\ \Rightarrow \left( {{a^u}} \right)' = u'.{a^u}.\ln a \end{array}\)
c) Đạo hàm của hàm số lôgarit
Chú ý:
\[\left( {\ln \left| x \right|} \right)' = \frac{1}{x}, \text{với mọi } x\ne 0.\]
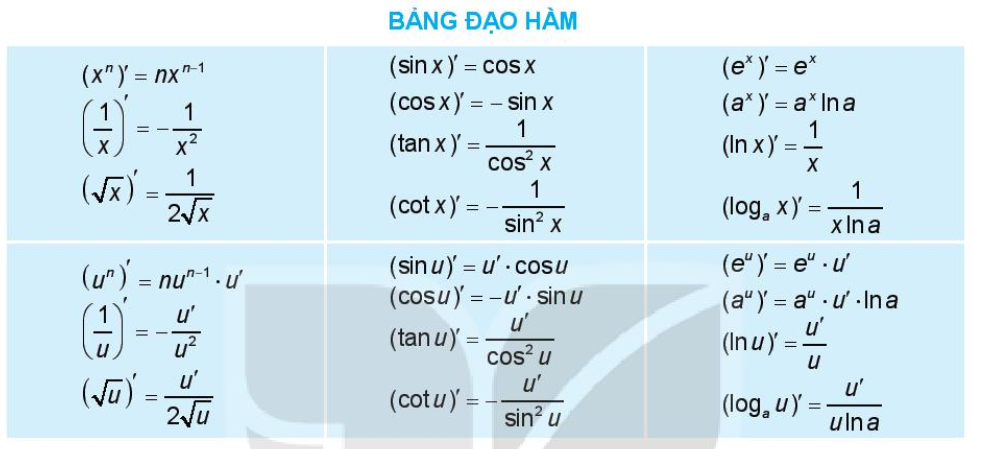
Như vậy, chúng ta có bảng đạo hàm cho các hàm cơ bản như sau:
Bài tập minh họa
Câu 1:
a) Cho hàm số f(x)=x6. Tính f'(x) và f'(1).
b) Tính đạo hàm của hàm số \(y=\sqrt x\) tại x=9.
Hướng dẫn giải:
a) Ta có: \(f'(x) = 6{x^5},\forall x \in \mathbb{R}\)
Vậy: \(f'(1) = 6.\)
b) Ta có: \(f'(x) = \frac{1}{{2\sqrt x }}\)
Tại x=9 ta có: \(f'(9) = \frac{1}{{2\sqrt 9 }} = \frac{1}{6}.\)
Câu 2: Tính đạo hàm của các hàm số sau:
a) \(y = \frac{1}{4}x + \frac{1}{x}.\)
b) \(y = \frac{{2x + 1}}{{x + 1}}.\)
c) \(y = \frac{{ - {x^2} + 2x + 3}}{{{x^3} - 2}}.\)
Hướng dẫn giải:
a) \(y' = \left( {\frac{1}{4}x + \frac{1}{x}} \right)' = \left( {\frac{1}{4}x} \right)' + \left( {\frac{1}{x}} \right)' = \frac{1}{4} - \frac{1}{{{x^2}}} = \frac{{{x^2} - 4}}{{4{x^2}}}.\)
b) \(y' = \left( {\frac{{2x + 1}}{{x + 1}}} \right)' = \frac{{(2x + 1)'(x + 1) - (2x + 1)(x + 1)'}}{{{{(x + 1)}^2}}} = \frac{1}{{{{(x + 1)}^2}}}.\)
c) \(y' = \left( {\frac{{ - {x^2} + 2x + 3}}{{{x^3} - 2}}} \right)' = \frac{{( - {x^2} + 2x + 3)'({x^3} - 2) - ( - {x^2} + 2x + 3)({x^3} - 2)'}}{{{{({x^3} - 2)}^2}}}\)
\(= \frac{{\left( { - 2x + 2} \right)({x^3} - 2) - 3{x^2}( - {x^2} + 2x + 3)}}{{{{({x^3} - 2)}^2}}} = \frac{{{x^4} - 4{x^3} - 9{x^2} + 4x - 4}}{{{{({x^3} - 2)}^2}}}.\)
Luyện tập Bài 32 Toán 11 Kết Nối Tri Thức
Học xong bài học này, em có thể:
- Tính đạo hàm của một số hàm số sơ cấp cơ bản. Sử dụng các công thức tính đạo hàm của tổng, hiệu, tích thương các hàm số và đạo hàm của hàm số hợp.
- Vận dụng các quy tắc đạo hàm để giải quyết một số bài toán thực tiễn.
3.1. Trắc nghiệm Bài 32 Toán 11 Kết Nối Tri Thức
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Kết nối tri thức Chương 9 Bài 32 cực hay có đáp án và lời giải chi tiết.
-
- A. 23
- B. 7
- C. -7
- D. -23
-
- A. \(\;\left( {8{x^3} - 6x - 5} \right)\left( {2x - 7} \right)\)
- B. \(\left( {8{x^3} - 6x - 5} \right)\left( {{x^2} - 7x} \right) - \left( {2{x^4} - 3{x^2} - 5x} \right)\left( {2x - 7} \right)\)
- C. \(\left( {8{x^3} - 6x - 5} \right)\left( {{x^2} - 7x} \right)+ \left( {2{x^4} - 3{x^2} - 5x} \right)\left( {2x - 7} \right)\)
- D. \(\;\left( {8{x^3} - 6x - 5} \right)+\left( {2x - 7} \right)\)
-
Câu 3:
Đạo hàm của hàm số \(y = \frac{{ - {x^2} - 2x + 5}}{{{x^3} - 1}}\) bằng biểu thức nào dưới đây?
- A. \(\frac{{ - 2x - 2}}{{3{x^2}}}\)
- B. \(\frac{{ - 2x - 2}}{{{{\left( {{x^3} - 1} \right)}^2}}}\)
- C. \(\frac{{ - 2x - 2 - 3{x^2}}}{{{{\left( {{x^3} - 1} \right)}^2}}}\)
- D. \(\frac{{\left( { - 2x - 2} \right)\left( {{x^3} - 1} \right) - 3{x^2}\left( { - {x^2} - 2x + 5} \right)}}{{{{\left( {{x^3} - 1} \right)}^2}}}\)
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 32 Toán 11 Kết Nối Tri Thức
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Kết nối tri thức Chương 9 Bài 32 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động 1 trang 88 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 2 trang 88 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 3 trang 88 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Luyện tập 1 trang 90 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 4 trang 90 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Luyện tập 2 trang 91 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 5 trang 91 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Luyện tập 3 trang 91 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 6 trang 91 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Luyện tập 4 trang 92 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 7 trang 92 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Luyện tập 5 trang 92 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 8 trang 92 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 9 trang 93 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Luyện tập 6 trang 93 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 10 trang 93 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Luyện tập 7 trang 94 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Vận dụng 2 trang 94 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 9.6 trang 94 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 9.7 trang 94 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 9.8 trang 94 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 9.9 trang 94 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 9.10 trang 94 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 9.11 trang 94 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 9.12 trang 94 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Bài tập 9.8 trang 60 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.9 trang 60 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.10 trang 60 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.11 trang 60 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.12 trang 60 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.13 trang 60 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.14 trang 60 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.15 trang 60 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.16 trang 60 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Hỏi đáp Bài 32 Toán 11 Kết Nối Tri Thức
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247