Bài tập 44 tr 130 sách GK Toán lớp 9 Tập 2
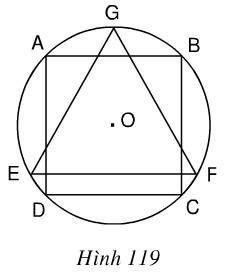
Cho hình vuông \(ABCD\) nội tiếp đường tròn tâm \(O\), bán kính \(R\) và \(GEF\) là tam giác đều nội tiếp đường tròn đó, \(EF\) là dây song song với \(AB\) (h.119). Cho hình đó quay quanh trục \(GO\). Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Thể tích hình trụ: \(V=\pi r^2 h.\)
+) Thể tích hình nón: \(V = \dfrac{1}{3}\pi {r^2}h.\)
+) Thể tích hình cầu: \(V = \dfrac{4}{3}\pi {r^3}.\)
+) Diện tích toàn phần của hình trụ: \({S_{tp}} = 2\pi rh + 2\pi {r^2}.\)
+) Diện tích toàn phần của hình nón: \({S_{tp}} = \pi rl + \pi {r^2}.\)
Lời giải chi tiết
Khi quay hình vẽ quanh trục \(GO\) ta được:
a) Thể tích hình trụ được tạo bởi hình vuông \(ABCD\) là:
\(\displaystyle V = \pi {\left( {{{AB} \over 2}} \right)^2}.BC\) với \(BC=AB = \sqrt {OA^2+OB^2}=\sqrt {2R^2}=R\sqrt2.\)
\(\eqalign{
& \Rightarrow V = \pi {\left( {{{R\sqrt 2 } \over 2}} \right)^2}.R\sqrt 2 \cr
& = \pi .{{2{{\rm{R}}^2}} \over 4}.R\sqrt 2 = {{\pi {{\rm{R}}^3}\sqrt 2 } \over 2} \cr
& \Rightarrow {V^2} = \left( {{{\pi {R^3}\sqrt 2 } \over 2}} \right)^2 = {{{\pi ^2}{R^6}} \over 2}(1) \cr}\)
Thể tích hình cầu có bán kính \(R\) là: \(\displaystyle {V_1} = {4 \over 3}\pi {R^3}\)
Thể tích hình nón có bán kính đường tròn đáy bằng \(\displaystyle {{EF} \over 2}\) là:
\(\displaystyle {V_2} = {1 \over 3}\pi {\left( {{{EF} \over 2}} \right)^2}.GH\)
Với \(EF = R\sqrt3\) (cạnh tam giác đều nội tiếp trong đường tròn \((O;R)\))
và \(\displaystyle GH = {{EF\sqrt 3 } \over 2} = {{R\sqrt {3.} \sqrt 3 } \over 2} = {{3R} \over 2}\)
Thay vào V2, ta có: \(\displaystyle {V_2} = {1 \over 3}\pi {\left( {{{R\sqrt 3 } \over 2}} \right)^2}.{{3{\rm{R}}} \over 2} = {3 \over 8}\pi {R^3}\)
Ta có: \(\displaystyle {V_1}{V_2} = {4 \over 3}\pi {R^3}.{3 \over 8}\pi {R^3} = {{{\pi ^2}{R^6}} \over 2}(2)\)
So sánh (1) và (2) ta được : \({V^2} = {V_1}.{V_2}\)
b) Diện tích toàn phần của hình trụ có bán kính \(\displaystyle {{AB} \over 2}\) là:
\(\eqalign{
& S = 2\pi \left( {{{AB} \over 2}} \right).BC + 2\pi {\left( {{{AB} \over 2}} \right)^2} \cr
& S = 2\pi .{{R\sqrt 2 } \over 2}R\sqrt 2 + 2\pi {\left( {{{R\sqrt 2 } \over 2}} \right)^2} \cr
& S = 2\pi {R^2} + \pi {R^2} = 3\pi {R^2} \cr
& \Rightarrow {S^2} = {\left( {3\pi {R^2}} \right)^2} = 9{\pi ^2}.{R^4}(1) \cr} \)
Diện tích mặt cầu có bán kính \(R\) là: \({S_1} = {\rm{ }}4\pi {R^2}\) (2)
Diện tích toàn phần của hình nón là:
\(\displaystyle {S_2} = \pi {{EF} \over 2}.FG + \pi {\left( {{{EF} \over 2}} \right)^2}\)
\(\displaystyle = \pi {{R\sqrt 3 } \over 2}.R\sqrt 3 + \pi {\left( {{{R\sqrt 3 } \over 2}} \right)^2} = {{9\pi {R^2}} \over 4}\)
Ta có: \(\displaystyle {S_1}{S_2} = 4\pi {R^2}.{{9\pi {R^2}} \over 4} = 9{\pi ^2}{R^4}(2)\)
So sánh (1) và (2) ta có: \({S^2} = {\rm{ }}{S_1}.{\rm{ }}{S_2}\)
-- Mod Toán 9 HỌC247
-


Cho biết hệ số góc của đường thẳng \(y = - 5x + 7\) là:
bởi Ban Mai
 11/07/2021
11/07/2021
A. \( - 5x\)
B. \(5\)
C. \( - 5\)
D. \(7\)
Theo dõi (0) 1 Trả lời -


Cho một hình chữ nhật có chu vi bằng 28 cm. Tính chiều dài và chiều rộng của hình chữ nhật, biết rằng nếu tăng chiều dài thêm 1 cm và tăng chiều rộng thêm 2 cm thì diện tích của hình chữ nhật đó tăng thêm 25 cm2.
bởi Nguyễn Minh Minh
 12/07/2021
12/07/2021
Cho một hình chữ nhật có chu vi bằng 28 cm. Tính chiều dài và chiều rộng của hình chữ nhật, biết rằng nếu tăng chiều dài thêm 1 cm và tăng chiều rộng thêm 2 cm thì diện tích của hình chữ nhật đó tăng thêm 25 cm2.
Theo dõi (0) 1 Trả lời -


Với hình chữ nhật ABCD với AB = 2a, BC = a. Khi quay hình chữ nhật ABCD quanh cạnh AB một vòng ta được hình trụ có thể tích V1 và khi quay hình chữ nhật ABCD quanh cạnh BC một vòng thì được hình trụ có thể tích V2. Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\)
bởi Tran Chau
 10/07/2021
10/07/2021
Với hình chữ nhật ABCD với AB = 2a, BC = a. Khi quay hình chữ nhật ABCD quanh cạnh AB một vòng ta được hình trụ có thể tích V1 và khi quay hình chữ nhật ABCD quanh cạnh BC một vòng thì được hình trụ có thể tích V2. Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\)
Theo dõi (0) 1 Trả lời -


Cho biết tam giác \(ABC\) vuông tại \(A,\;\;\widehat {ACB} = {30^0},\;\;AB = 5cm.\) Độ dài cạnh \(AC\) là:
bởi hi hi
 10/07/2021
10/07/2021
A. \(10cm\)
B. \(\dfrac{{5\sqrt 3 }}{2}cm\)
C. \(5\sqrt 3 cm\)
D. \(\dfrac{5}{{\sqrt 3 }}cm\)
Theo dõi (0) 1 Trả lời -


Cho đường tròn tâm O, đường kính AB = 2R. Trên đường tròn (O) lấy điểm C bất kì (C không trùng với A và B). Tiếp tuyến của đường tròn (O) tại A cắt tia BC ở điểm D. Gọi H là hình chiếu của A trên đường thẳng DO. Tia AH cắt đường tròn (O) tại điểm F (không trùng với A). Hãy chứng minh \(D{A^2} = DC.DB\)
bởi Anh Trần
 10/07/2021
10/07/2021
Cho đường tròn tâm O, đường kính AB = 2R. Trên đường tròn (O) lấy điểm C bất kì (C không trùng với A và B). Tiếp tuyến của đường tròn (O) tại A cắt tia BC ở điểm D. Gọi H là hình chiếu của A trên đường thẳng DO. Tia AH cắt đường tròn (O) tại điểm F (không trùng với A). Hãy chứng minh \(D{A^2} = DC.DB\)
Theo dõi (0) 1 Trả lời -


Với đường tròn tâm O bán kính 2R (kí hiệu (O; 2R)) và đường tròn tâm O’ bán kính R (kí hiệu (O’; R)) tiếp xúc ngoài nhau tại A. Lấy điểm B trên đường tròn (O; 2R) sao cho \(\widehat {BAO} = {30^0}\), tia BA cắt đường tròn (O’; R) tại điểm C (C khác điểm A). Tiếp tuyến của đường tròn (O’; R) tại điểm C cắt đường thẳng BO tại điểm E. Tính theo R diện tích tam giác ABE.
bởi Duy Quang
 10/07/2021
10/07/2021
Với đường tròn tâm O bán kính 2R (kí hiệu (O; 2R)) và đường tròn tâm O’ bán kính R (kí hiệu (O’; R)) tiếp xúc ngoài nhau tại A. Lấy điểm B trên đường tròn (O; 2R) sao cho \(\widehat {BAO} = {30^0}\), tia BA cắt đường tròn (O’; R) tại điểm C (C khác điểm A). Tiếp tuyến của đường tròn (O’; R) tại điểm C cắt đường thẳng BO tại điểm E. Tính theo R diện tích tam giác ABE.
Theo dõi (0) 1 Trả lời -


Với tam giác ABC có ba góc nhọn \(\left( {AB < AC} \right)\) và có đường cao AH (H thuộc cạnh BC). Gọi D, E lần lượt là trung điểm của AB và AC. Chứng minh DE là tiếp tuyến chung của hai đường tròn lần lượt ngoại tiếp tam giác DBH và ECH.
bởi Phung Hung
 10/07/2021
10/07/2021
Với tam giác ABC có ba góc nhọn \(\left( {AB < AC} \right)\) và có đường cao AH (H thuộc cạnh BC). Gọi D, E lần lượt là trung điểm của AB và AC. Chứng minh DE là tiếp tuyến chung của hai đường tròn lần lượt ngoại tiếp tam giác DBH và ECH.
Theo dõi (0) 1 Trả lời -


Với tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\;\left( {H \in BC} \right).\)Biết \(AB = 3a,\;\;AH = \dfrac{{12}}{5}a.\) Tính theo \(a\) độ dài \(AC\) và \(BC.\)
bởi Anh Nguyễn
 10/07/2021
10/07/2021
Với tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\;\left( {H \in BC} \right).\)Biết \(AB = 3a,\;\;AH = \dfrac{{12}}{5}a.\) Tính theo \(a\) độ dài \(AC\) và \(BC.\)
Theo dõi (0) 1 Trả lời -


Cho đường tròn tâm (O), từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB (A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D; O và B nằm về hai phía so với cát tuyến MCD). Hãy chứng minh tứ giác MAOB nội tiếp.
bởi Hương Lan
 10/07/2021
10/07/2021
Cho đường tròn tâm (O), từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB (A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D; O và B nằm về hai phía so với cát tuyến MCD). Hãy chứng minh tứ giác MAOB nội tiếp.
Theo dõi (0) 1 Trả lời -


Với tam giác ABC vuông tại A, đường cao AH \(\left( {H \in BC} \right)\) . Biết AC = 8cm và BC = 10 cm. Tính độ dài AB, BH, CH và AH.
bởi Nguyễn Ngọc Sơn
 10/07/2021
Theo dõi (0) 1 Trả lời
10/07/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 42 trang 130 SGK Toán 9 Tập 2
Bài tập 43 trang 130 SGK Toán 9 Tập 2
Bài tập 42 trang 174 SBT Toán 9 Tập 2
Bài tập 43 trang 174 SBT Toán 9 Tập 2
Bài tập 44 trang 174 SBT Toán 9 Tập 2
Bài tập 45 trang 174 SBT Toán 9 Tập 2
Bài tập 46 trang 175 SBT Toán 9 Tập 2
Bài tập 47 trang 175 SBT Toán 9 Tập 2
Bài tập 48 trang 175 SBT Toán 9 Tập 2
Bài tập 49 trang 175 SBT Toán 9 Tập 2
Bài tập IV.1 trang 176 SBT Toán 9 Tập 2
Bài tập IV.2 trang 176 SBT Toán 9 Tập 2
Bài tập IV.3 trang 176 SBT Toán 9 Tập 2
Bài tập IV.4 trang 177 SBT Toán 9 Tập 2





