Bài tập 48 trang 175 SBT Toán 9 Tập 2
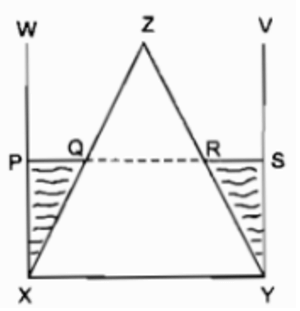
Hình bên (h.113) gồm một hình nón được đặt khít vào bên trong một cốc hình trụ, chúng có cùng đáy, cùng chiều cao. Người ta đổ vào đó một lượng nước lên đến một nửa chiều cao của hình. (Giả sử rằng nước không rò rỉ, không thẩm thấu vào bên trong hình nón)
Hãy chọn đúng tỉ số giữa các đoạn thẳng QR/XY
(A) \(\frac{1}{2}\);
(B) \(\frac{1}{3}\);
(C) \(\frac{2}{3}\)
(D) Không tính được, vì câu hỏi phụ thuộc vào bán kính đáy
Hướng dẫn giải chi tiết
Vì hình trụ và hình nón có cùng chiều cao, người ta đổ nước lên đến nửa chiều cao của hình nên Q là trung điểm của xz, R là trung điểm của yz
Nên \(\frac{QR}{XY}\) = \(\frac{1}{2}\)
Chọn (A) \(\frac{1}{2}\)
-- Mod Toán 9 HỌC247
-


Cho đa giác đều 24 cạnh A1A2...A24. Tỷ số bán kính đường tròn ngoại tiếp và đường tròn nội tiếp tam giác A1A9A13 bằng bao nhiêu?
bởi Minh Đức
 02/04/2020
02/04/2020
Cho đa giác đều 24 cạnh A1A2...A24. Tỷ số bán kính đường tròn ngoại tiếp và
đường tròn nội tiếp tam giác A1A9A13 bằng bao nhiêu?
Theo dõi (0) 1 Trả lời -


Cho ∆ABC nhọn nội tiếp đường tròn (O). Gọi M là một điểm trên cung nhỏ BC (M khác B, C và AM không đi qua O). Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M. Gọi D là điểm đối xứng với M qua O. Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng ba điểm N, P, D thẳng hàng.
bởi Phươngg Linhh
 01/04/2020
01/04/2020
BÀI 1.Cho ∆ABC nhọn nội tiếp đường tròn (O). Gọi M là một điểm trên cung nhỏ BC (M khác B, C và AM không đi qua O). Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M. Gọi D là điểm đối xứng với M qua O. Đường tròn đường kính MP cắt MD tại điểm Q khác M.
a/ Chứng minh rằng ba điểm N, P, D thẳng hàng.
b/ Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Theo dõi (1) 1 Trả lời -


Cho đường tròn (O) đường kính AB.Một điểm P bên ngoài (O) và PA, PB lần lượt cắt đường tròn tại M và N. Chứng minh PA. PM = PB. PN
bởi Nguyễn Lê
 30/03/2020
30/03/2020
Cho đường tròn (O) đường kính AB.Một điểm P bên ngoài (O) và PA, PB lần lượt cắt đường tròn tại M và N. a) Chứng minh PA. PM = PB. PN b)Gọi H là giao điểm của AN và BM. Chứng minh PH vuông góc AB.
Theo dõi (0) 1 Trả lời -


Cho đường tròn (O) đường kính AB. Vẽ dây CD vuông góc với đường kính AB tại H. Gọi M là điểm chính giữa cung nhỏ CB, I là giao điểm của CB và OM. Chứng minh: a. MA là tia phân giác CMD
bởi Trần Minh
 27/03/2020
27/03/2020
Cho đường tròn (O) đường kính AB. Vẽ dây CD vuông góc với đường kính AB tại H. Gọi M là điểm chính giữa cung nhỏ CB, I là giao điểm của CB và OM. Chứng minh: a. MA là tia phân giác CMD b. Bốn điểm O, H, C, I cùng nằm trên một đường tròn. c. Đường vuông góc vẽ từ M đến AC cũng là tiếp tuyến của đường tròn (O) tại M.
Theo dõi (0) 1 Trả lời -


Viết phương trình đường thẳng đi qua hai điểm A(2;-2) và B(1-4) và tìm giao điểm của đường thẳng vừa tìm được với đồ thị hàm số y=1/2x^2
bởi Kim Oanh
 26/03/2020
26/03/2020
1.Vẽ đồ thị hàm số:y=1/2x^2 a,Viết phương trình đường thẳng đi qua hai điểm A(2;-2) và B(1-4) b,Tìm giao điểm của đường thẳng vừa tìm được với đồ thị trên 2,Cho (P) y=- x^2/4 và đường thẳng (d) y =x+m a,Vẻ(P) b,Xác định m để (P) và (d) cắt nhau tại hai điểm phân biệt A và B c,Xác định phương trình đường thẳng (d') song song với đường thẳng (d) và cắt (P) tại điểm có tung độ bằng -4 3,Cho (P): y = 1/4x^2 và đường thẳng (D) qua 2 điểm A và B trên (P) có hoành độ lần lượt là -2 và 4 a,Vẽ đồ thị (P) của hàm số trên b) Viết phương trình của (D) c) Tìm điểm M trên cung AB của (P) (tương ứng hoành độ) x € [-2;4] sao cho tam giác MAB có diện tích lớn nhất
Theo dõi (0) 2 Trả lời -


Cho tam giác ABC cân tại A nội tiếp đường tròn (O) đường kính AD. Các tiếp tuyến của đường tròn tại B và C cắt nhau tại K. Gọi E là giao điểm của BD và AC. Chứng minh góc KBD= góc KAC
bởi Khánh Linh
 20/03/2020
20/03/2020
Cho tam giác ABC cân tại A nội tiếp đường tròn (O) đường kính AD. Các tiếp tuyến của đường tròn tại B và C cắt nhau tại K. Gọi E là giao điểm của BD và AC
a) Chứng minh góc KBD= góc KAC
b) Bốn điểm A, B, K, E cùng thuộc một đường tròn
c) KE =KB
Mọi người giúp em với ạ. Em cảm ơnTheo dõi (0) 0 Trả lời -


Cho đường tròn (O; R). Một điểm A ở ngoài đường tròn sao cho OA = 2R. Vẽ các tiếp tuyến AB và AC đến (O) ( A , B là hai tiếp điểm). Tính số đo các góc AOB và góc BOC .
bởi Lê Minh Ngọc
 19/03/2020
19/03/2020
Cho đường tròn (O; R). Một điểm A ở ngoài đường tròn sao cho OA = 2R. Vẽ các tiếp tuyến AB và AC đến (O) ( A , B là hai tiếp điểm).
a) Tính số đo các góc AOB và góc BOC .
b) Tính số đo cung nhỏ và cung lớn BC.
Theo dõi (0) 4 Trả lời -


Chứng minh DE là tiếp tuyến chung của hai đường tròn
bởi Hân Hân
 16/03/2020
16/03/2020
cho tam giác ABC vuông tại A đường cao AH . đường tròn đường kính BH cắt AB tại D và đường tròn đường kính CH cắt AC tại E . CMR : DE là tiếp tuyến chung của (I) và (J)
Theo dõi (0) 0 Trả lời -


Cho đường tròn (O; R), dây CD khác 2R cố định. Trên tia đối của tia CD lấy điểm M. Từ M kẻ hai tiếp tuyến MA, MB ( A; B thuộc đường tròn, A thuộc cung lớn CD). Đoạn thẳng OM cắt AB tại E, cắt đường tròn tại F. a) Chứng minh tứ giác AOBM nội tiếp.
bởi Vũ Đức
 09/03/2020
09/03/2020
Cho đường tròn (O; R), dây CD khác 2R cố định. Trên tia đối của tia CD lấy điểm M. Từ M kẻ hai tiếp tuyến MA, MB ( A; B thuộc đường tròn, A thuộc cung lớn CD). Đoạn thẳng OM cắt AB tại E, cắt đường tròn tại F.
a) Chứng minh tứ giác AOBM nội tiếp.
b) Chứng minh: MA2=MC. MD
c) Chứng minh điểm F cách đều 3 cạnh của tam giác ABM.
d) Chứng minh góc CED không đổi khi M chuyển động trên tia đối của tia CD.Theo dõi (0) 0 Trả lời -


Cho tam giác ABC nhọn (). Đường tròn tâm O đường kính BC cắt AB, AC theo thứ tự tại N và M. a) Chứng minh AN.AB = AD.AC;
bởi Trả Tiền Cho Teo
 08/03/2020
08/03/2020
Cho tam giác ABC nhọn (). Đường tròn tâm O đường kính BC cắt AB, AC theo thứ tự tại N và M.
a) Chứng minh AN.AB = AD.AC;
b) Gọi H là giao điểm của BM và CN; gọi K là giao điểm của AH và BC.Chứng minh ;
c) Kẻ tiếp tuyến AP, AQ đến đường tròn (O); P và Q là các tiếp điểm. Chứng minh các điểm A, P, K, O, Q cùng thuộc một đường tròn;
d) Chứng minh: đồng dạng ; ba điểm P, H, Q thẳng hàng
Theo dõi (1) 3 Trả lời
Bài tập SGK khác
Bài tập 46 trang 175 SBT Toán 9 Tập 2
Bài tập 47 trang 175 SBT Toán 9 Tập 2
Bài tập 49 trang 175 SBT Toán 9 Tập 2
Bài tập IV.1 trang 176 SBT Toán 9 Tập 2
Bài tập IV.2 trang 176 SBT Toán 9 Tập 2
Bài tập IV.3 trang 176 SBT Toán 9 Tập 2
Bài tập IV.4 trang 177 SBT Toán 9 Tập 2