Với bài học này chúng ta sẽ cùng tìm hiểu về cách tính Diện tích hình thang, cùng với các ví dụ minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng làm chủ nội dung bài học.
Tóm tắt lý thuyết
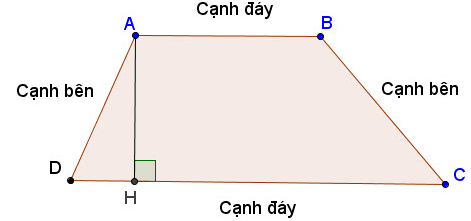
1.1. Công thức tính diện tích hình thang
Trước tiên tính công thức chung của hình thang chúng ta sẽ có công thức: trung bình cộng 2 cạnh đáy nhân với chiều cao giữa 2 đáy
S = 1/2(a+b) * h
1.2. Công thức tính diện tích hình bình hành
Diện tích hình bình hành bằng tích một cạnh nhân với đường cao tương ứng \(S = a.h\)
.png)
Bài tập minh họa
Bài 1: Cho hình thang ABCD có E,F lần lượt là trung điểm của hai canh bên BC,AD. Gọi G là trung điểm của EF. qua G kẻ đường thẳng bất kì cắt AB tại H và CD tại I. Chứng mình rằng : \({S_{AHI{\rm{D}}}} = {S_{HBCI}}\)
Hướng dẫn:
.png)
Ta dễ dàng chứng minh được G là trung điểm của HI.
Gọi h là độ dài đường cao của hình thang dễ thấy rằng hai hình thang AHID và HBCI có đường cao có độ dài là h.
Xét hình thang AHID có:
\(EG = \frac{{AH + I{\rm{D}}}}{2}\) (EG là đường trung bình của hình thang AHID)
\({S_{AHI{\rm{D}}}} = \frac{{AH + I{\rm{D}}}}{2}.h = EG.h\) (1)
tương tự với hình thang HBCI ta có:
\(GF = \frac{{BH + CI}}{2}\) (GF là đường trung bình của hình thang HBCI)
\({S_{HBCI}} = \frac{{BH + CI}}{2}.h = GF.h\) (2)
mà EG=GF(G trung điểm EF) (3)
Từ (1),(2) và (3) ta được: \({S_{AHI{\rm{D}}}} = {S_{HBCI}}\)
Bài 2: Hình thang cân ABCD (\(AB\parallel C{\rm{D}}\))có độ dài đường cao là h và hai đường chéo vuông góc với nhau. Tính diện tích hình thang đó theo h.
Hướng dẫn:
.png)
Gọi E là giao điểm của hai đường chéo, qua E kẻ đường thẳng vuông góc với AB và cắt AB tại F, cắt CD tại G., Theo đề bài ta có FG=h.
Dễ thấy rằng hai tam giác ABD và BAC bằng nhau (trường hợp cạnh - góc - cạnh) nên \(\widehat {{\rm{ABD}}} = \widehat {BAC}\) ⇒ ABE là tam giác vuông cân tại E
mà EF là đường cao đồng thời là đường trung tuyến ⇒ \(EF = \frac{1}{2}AB \Rightarrow AB = 2EF\)
Tương tự ta cũng có EDC là tâm giác vuông cân tại E với EG là đường cao đồng thời là trung tuyến \( \Rightarrow EG = \frac{1}{2}CD \Rightarrow CD = 2EG\)
Ta được AB+CD=2EF+2EG=2(EF+EG)=2FG=2h.
Diện tích hình thang ABCD là \(S = \frac{{AB + C{\rm{D}}}}{2}h = \frac{{2h}}{2}h = {h^2}\) (đơn vị diện tích)
3. Luyện tập Bài 4 Chương 2 Hình học 8
Qua bài giảng Diện tích hình thang này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
- Nắm vững công thức tính diện tích hình thanh, diện tích hình bình hành
- Vận dụng kiến thức đã học làm được một số bài toán liên quan
3.1 Trắc nghiệm về Diện tích hình thang
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Hình học 8 Bài 4 cực hay có đáp án và lời giải chi tiết.
-
- A. 20cm
- B. 16cm
- C. 15cm
- D. 12cm
-
- A. 5cm
- B. 4cm
- C. 4,5cm
- D. 9cm
-
- A. AB.AD
- B. (AB + DC).AD
- C. \(\frac{1}{2}\left( {AB + C{\rm{D}}} \right)\)
- D. \(\frac{1}{2}A{\rm{D}}.\left( {AB + C{\rm{D}}} \right)\)
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2. Bài tập SGK về Diện tích hình thang
Các em có thể xem thêm phần hướng dẫn Giải bài tập Hình học 8 Bài 4 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Bài tập 26 trang 125 SGK Toán 8 Tập 1
Bài tập 27 trang 125 SGK Toán 8 Tập 1
Bài tập 28 trang 126 SGK Toán 8 Tập 1
Bài tập 29 trang 126 SGK Toán 8 Tập 1
Bài tập 30 trang 126 SGK Toán 8 Tập 1
Bài tập 31 trang 126 SGK Toán 8 Tập 1
Bài tập 32 trang 161 SBT Toán 8 Tập 1
Bài tập 33 trang 161 SBT Toán 8 Tập 1
Bài tập 34 trang 161 SBT Toán 8 Tập 1
Bài tập 35 trang 161 SBT Toán 8 Tập 1
Bài tập 36 trang 161 SBT Toán 8 Tập 1
Bài tập 37 trang 162 SBT Toán 8 Tập 1
Bài tập 38 trang 162 SBT Toán 8 Tập 1
Bài tập 39 trang 162 SBT Toán 8 Tập 1
Bài tập 40 trang 162 SBT Toán 8 Tập 1
Bài tập 41 trang 162 SBT Toán 8 Tập 1
Bài tập 4.1 trang 162 SBT Toán 8 Tập 1
Bài tập 4.2 trang 162 SBT Toán 8 Tập 1
Bài tập 4.3 trang 162 SBT Toán 8 Tập 1
Bài tập 32 trang 161 SBT Toán 8 Tập 1
Bài tập 33 trang 161 SBT Toán 8 Tập 1
Bài tập 34 trang 161 SBT Toán 8 Tập 1
Bài tập 35 trang 161 SBT Toán 8 Tập 1
Bài tập 36 trang 161 SBT Toán 8 Tập 1
Bài tập 37 trang 162 SBT Toán 8 Tập 1
Bài tập 38 trang 162 SBT Toán 8 Tập 1
Bài tập 39 trang 162 SBT Toán 8 Tập 1
Bài tập 40 trang 162 SBT Toán 8 Tập 1
Bài tập 41 trang 162 SBT Toán 8 Tập 1
Bài tập 4.1 trang 162 SBT Toán 8 Tập 1
Bài tập 4.2 trang 162 SBT Toán 8 Tập 1
Bài tập 4.3 trang 162 SBT Toán 8 Tập 1
4. Hỏi đáp Bài 4 Chương 2 Hình học 8
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 8 HỌC247





.PNG)







