Giải bài 37 tr 162 sách BT Toán lớp 8 Tập 1
Chứng minh rằng mọi đường thẳng đi qua trung điểm của đường trung bình của hình thang và cắt hai đáy hình thang sẽ chia hình thang đó thành hai hình thang có diện tích bằng nhau.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Áp dụng tính chất đường trung bình của hình thang bằng nửa tổng hai đáy.
Công thức tính diện tích hình thang: \(S=\dfrac{a+b}{2}.h\)
Lời giải chi tiết
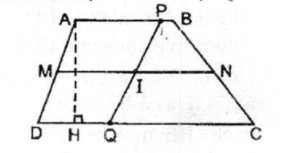
Giả sử hình thang \(ABCD\) có \(AB // CD,\) đường trung bình là \(MN.\) Gọi \(I\) là trung điểm của \(MN,\) đường thẳng bất kỳ đi qua \(I\) cắt \(AB\) tại \(P\) và \(CD\) tại \(Q\)
Ta có hai hình thang \(APQD\) và \(BPQC\) có chung đường cao.
\(MI\) là đường trung bình của hình thang \(APQD:\)
\( \Rightarrow MI = \dfrac{1} {2}\left( {AP + QD} \right)\)
\(IN\) là đường trung bình của hình thang \(BPQC :\)
\( \Rightarrow IN = \dfrac{1} {2}\left( {BP + QC} \right)\)
\(S_{APQD}=\dfrac{1}{2}\ \left( {AP + QD} \right).AH\) \(=MI.AH\) \((1)\)
\(S_{BPQC}=\dfrac{1}{2}\ \left( {BP + QC} \right).AH\) \(=NI.AH\) \((2)\)
\(IM = IN\) (gt) \((3)\)
Từ \((1),\, (2)\) và \((3)\) suy ra : \({S_{APQD}} = {S_{BPQC}}\) không phụ thuộc vào \(P\) và \(Q\)
-- Mod Toán 8 HỌC247
-


Diện tích hình thang
bởi Lê Nhật Minh
 24/07/2018
24/07/2018
Từ công thức tính diện tích hình thang có thể suy ra công thức tính diện tích tam giác ,hình chữa nhật, hình vuông được k?
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 35 trang 161 SBT Toán 8 Tập 1
Bài tập 36 trang 161 SBT Toán 8 Tập 1
Bài tập 38 trang 162 SBT Toán 8 Tập 1
Bài tập 39 trang 162 SBT Toán 8 Tập 1
Bài tập 40 trang 162 SBT Toán 8 Tập 1
Bài tập 41 trang 162 SBT Toán 8 Tập 1
Bài tập 4.1 trang 162 SBT Toán 8 Tập 1





