Giải bài 30 tr 126 sách GK Toán 8 Tập 1
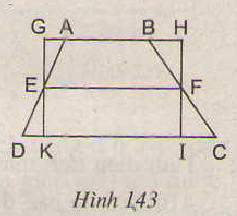
Trên hình 143 ta có hình thang ABCD với đường trung bình EF và hình chữ nhật GHIK. Hãy so sánh dện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang.
Hướng dẫn giải chi tiết
Ta có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
\(\Delta AEK = \Delta DEK, \Delta EFH = \Delta CFI\)
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà \(EF = \frac{AB+CD}{2}\)
Do đó \(S_{ABCD}= \frac{AB+CD}{2}\) ( AB + CD). AJ
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.
-- Mod Toán 8 HỌC247
-
Cho hình thang ABCD có đáy nhỏ AB là 27 cm, đáy lớn CD là 48 cm. Nếu kéo dài đáy nhỏ thêm 5 cm thì S của hình tăng 40 cm². Tính S hình thang đã cho.
Theo dõi (0) 1 Trả lời -
Tính diện tích hình thang ABCD biết AB=32 cm, AD=0,3 m
bởi Duy Quang
10/10/2018
Cho hình thang ABCD (vuông ở A và D) có cạnh đáy bé là AB và cạnh đáy lớn là DC.Từ B hạ đường cao BH vuông góc với cạnh đáy lớn DC.Tính diện tích hình thang ABCD biết canhjAB dài 32 cm,cạnh AD dài 0,3m và cạnh HC dài 2dm.
Theo dõi (0) 1 Trả lời
