Bài tập 38 trang 162 SBT Toán 8 Tập 1
Diện tích hình bình hành bằng 24cm2. Khoảng cách từ giao điểm hai đường chéo đến các cạnh hình bình hành bằng 2cm và 3cm. Tính chu vi của hình bình hành.
Hướng dẫn giải chi tiết
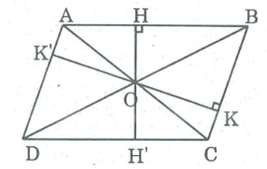
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2cm , đến cạnh BC là OK = 3cm
* Kéo dài OH cắt cạnh CD tại H'.
Ta có OH ⊥ BC
=> OH' ⊥ CD và OH' = 2cm
Suy ra HH' bằng đường cao của hình bình hành.
SABCD = HH'.AB => \(AB = \frac{{{S_{ABCD}}}}{{HH'}} = \frac{{24}}{4} = 6\left( {cm} \right)\)
* Kéo dài OK cắt AD tại K'.
Ta có: OK ⊥ BC => OK' ⊥ CD và OK' = 3 (cm)
Suy ra KK' là đường cao của hình bình hành.
SABCD = KK'.AB => \(BC = \frac{{{S_{ABCD}}}}{{KK'}} = \frac{{24}}{6} = 4\left( {cm} \right)\)
Chu vi của hình bình hành ABCD là (6 + 4).2 = 20 (cm).
-- Mod Toán 8 HỌC247
-


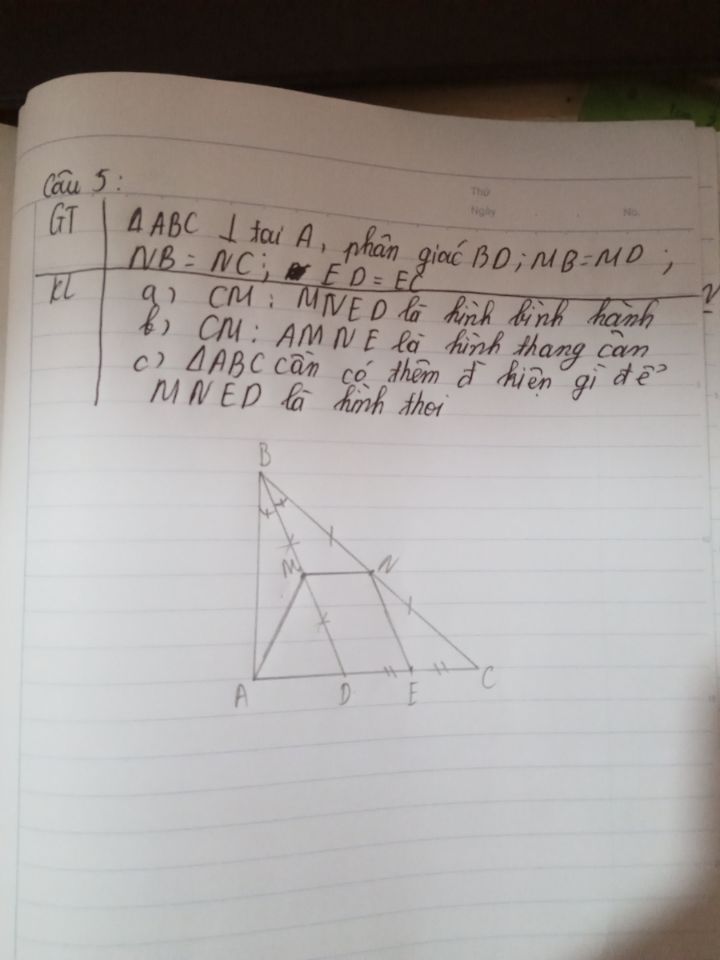
Cho tam giác ABC vuông tại A, phân giác BD, điểm M là trung điểm của BD, N là trung điểm BC; ED=EC. Chứng minh MNEC là hình bình hành.
bởi Đường Việt
 26/02/2020
26/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Bài toán hình bình hành
bởi Thùy Hồ
 14/12/2019
14/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 36 trang 161 SBT Toán 8 Tập 1
Bài tập 37 trang 162 SBT Toán 8 Tập 1
Bài tập 39 trang 162 SBT Toán 8 Tập 1
Bài tập 40 trang 162 SBT Toán 8 Tập 1
Bài tập 41 trang 162 SBT Toán 8 Tập 1
Bài tập 4.1 trang 162 SBT Toán 8 Tập 1
Bài tập 4.2 trang 162 SBT Toán 8 Tập 1
Bài tập 4.3 trang 162 SBT Toán 8 Tập 1
Bài tập 32 trang 161 SBT Toán 8 Tập 1
Bài tập 33 trang 161 SBT Toán 8 Tập 1
Bài tập 34 trang 161 SBT Toán 8 Tập 1
Bài tập 35 trang 161 SBT Toán 8 Tập 1
Bài tập 36 trang 161 SBT Toán 8 Tập 1
Bài tập 37 trang 162 SBT Toán 8 Tập 1
Bài tập 38 trang 162 SBT Toán 8 Tập 1
Bài tập 39 trang 162 SBT Toán 8 Tập 1
Bài tập 40 trang 162 SBT Toán 8 Tập 1
Bài tập 41 trang 162 SBT Toán 8 Tập 1
Bài tập 4.1 trang 162 SBT Toán 8 Tập 1