Bài tập 4.2 trang 162 SBT Toán 8 Tập 1

Hướng dẫn giải

a) Chứng minh \(∆ DFC = ∆ EFB \,(g.c.g)\)

b) Gọi \(K\) là trung điểm của \(AE,\) nối \(K\) với \(D.\) Từ đó chia hình hợp lí để hình thang đã cho chia thành hai phần có diện tích bằng nhau.

Lời giải chi tiết

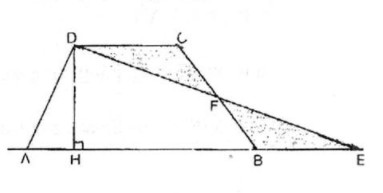
a. Gọi F là trung điểm của cạnh bên BC. Cắt hình thang theo đường DF đưa ghép về như hình vẽ bên, điểm C trung với điểm B, D trùng với E.

Vì AB // CD \( \Rightarrow \widehat {ABC} + 180^\circ   \Rightarrow {\rm A},{\rm B},{\rm E}\) thẳng hàng

\(\widehat {ABF} + \widehat {DFC} = 180^\circ \)

⇒ D, F, E thẳng hàng

∆ DFC = ∆ EFB (g.c.g)

\({S_{DFC}} = {S_{EFB}}\)

Suy ra: \({S_{ABCD}} = {S_{ADE}}\)

∆ DFC = ∆ EFB⇒ DC = BE

AE = AB + BE = AB + DC

\({S_{ADE}} = {1 \over 2}DH.AE = {1 \over 2}DH.\left( {AB + CD} \right)\)

Vậy : \({S_{ABCD}} = {1 \over 2}DH.\left( {AB + CD} \right)\)

b. Dựa trên hình vẽ câu a ta chọn điểm K là trung điểm AE.

Ta nối DK cắt hình thang theo đường DK ta có hai phần diện tích bằng nhau:

Một phần là ∆ ADK có \(AK = {{AB + CD} \over 2}\)

Một phần là hình thang BCDK có hai đáy CD + BK = \({{AB + CD} \over 2}\)

Và có chiều cao bằng nhau nên có diện tích bằng nhau.

-- Mod Toán 8 HỌC247