Giải bài 6 tr 137 sách BT Toán lớp 7 Tập 1
Cho tam giác \(ABC\) có \(\widehat B = \widehat C = 50^\circ \). Gọi tia \(Am\) là tia phân giác của góc ngoài ở đỉnh \(A.\) Hãy chứng tỏ \(Am // BC\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Góc ngoài tam giác bằng tổng hai góc trong không kề với nó.
- Nếu đường thẳng \(c\) cắt hai đường thẳng \(a, b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc cặp góc đồng vị bằng nhau, hoặc cặp góc trong cùng phía bù nhau) thì \(a\) và \(b\) song song với nhau.
Lời giải chi tiết
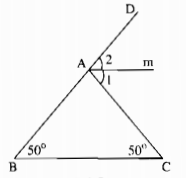
Trong ∆ABC, ta có: \(\widehat {CA{\rm{D}}}\) là góc ngoài tại đỉnh A
\(\widehat {CAD}{\rm{ = }}\widehat B + \widehat C = 50^\circ + 50^\circ = 100^\circ \) (tính chất góc ngoài của tam giác)
\(\widehat {{A_1}} = \widehat {{A_2}} = {1 \over 2}\widehat {CA{\rm{D}}} = 50^\circ \) (Vì tia Am là tia phân giác của \(\widehat {CA{\rm{D}}}\))
Suy ra: \(\widehat {{A_1}} = \widehat C = 50^\circ \)
\( \Rightarrow \) Am // BC (Vì có cặp góc ở vị trí so le trong bằng nhau)
-- Mod Toán 7 HỌC247
-
1. Cho tam giác ABC có góc B=80độ ; góc 3A=góc 2C . Tính gócA ; gócC
2. Cho tam giác ABC có góc A=90độ ; góc B=60độ. Tia phân giác góc A cắt BC tại D. Kẻ AH vuông góc BC (H thuộc BC)
a) Tính góc C
b) góc ADH ;góc HAD
Theo dõi (0) 1 Trả lời -
1. Cho tam giác ABC có góc A = 50độ ; góc B = 70độ. Tia phân giác góc C cắt AB tại M.
Tính góc AMC; góc BMC
2. Cho tam giác ABC có góc A = 100độ ; góc B - góc C =50độ
Tính góc B ; góc C
Theo dõi (0) 1 Trả lời -
Tinh góc C biết tam giác ABC vuông tại A có góc B=40 độ
bởi truc lam
04/04/2019
cho tam giác abc vuông tại a có góc b=400
a,tính góc c
b, gọi m là trungđiểm bc,trên tia đối của tia mc lấy điểm k sao cho mk=mc
c,CMR:tam giác acm =tam giác bkm
d,CMR:kb vuông góc ab
Theo dõi (0) 1 Trả lời -
Tính góc AHD biết tam giác ABC có góc B=70 độ, góc C=30 độ, AH vuông góc BC
bởi Trần Hoàng Mai
04/04/2019
Cho tam giác ABC có góc B=70, góc C=30. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC (H thuộc BC)
a) Tính góc BAC; b) Tính góc AHD; c) Tính góc HAD
Theo dõi (0) 1 Trả lời -
giúp mik vs
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H\(\in\) BC)*. Tìm góc bằng góc B
Theo dõi (0) 1 Trả lời -
Tính tổng số đo các góc của một hình chữ nhật
bởi hi hi
04/04/2019
+) Ko dùng thước đo góc, cho biết tổng số đo các góc của một hình chữ nhật.
+) Ko dùng thước đo góc, cho biết tổng số đo các góc trong một hình tứ giác lồi.
+) Có hay ko một tam giác mà cả 3 góc đều lớn hơn 60* ?
+) Có hay ko một tam giác mà cả 3 góc đều nhỏ hơn 60* ?
Theo dõi (0) 1 Trả lời -
Tính góc HAD biết tam giác ABC có góc B=70 độ, C=30 độ, AH vuông góc BC
bởi Nguyễn Thị Thanh
04/04/2019
Cho tam giác ABC có góc B = 70 độ, góc C = 30 độ. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC ( H thuộc BC )
a) Tính góc BAC
b) Tính góc ADH
c) Tính góc HAD
Theo dõi (0) 1 Trả lời -
Chứng minh Ax và Ay là 2 tia đối nhau biết góc CAx=góc ACB, góc BAy=góc ABC
bởi Việt Long
04/04/2019
Cho tam giác ABC.Trên nửa mặt phẳng AC không chứa điểm B,vẽ tia à sao cho \(\widehat{CAx}\)=\(\widehat{ACB}\).Trên nửa mặt phẳng bờ AB ko chứa điểm C,vẽ tia Ay sao cho \(\widehat{BAy}\)=\(\widehat{ABC}\).Chứng minh Ax và Ay là 2 tia đối nhau.
Theo dõi (0) 1 Trả lời -
cho \(\Delta\)ABC có góc B=70*, góc C=30*
a) vẽ đường cao AH vuông với BC
tính góc HAC, và góc HAB
b) vẽ tia phân giác góc A cắt B tại D
Tính góc ADC, và góc ADB
Theo dõi (0) 1 Trả lời -
Tính góc A, B, C của tam giác ABC có C:B:A=1:2:6
bởi Bánh Mì
06/04/2019
Giúp mình với mấy cậu ơi!!!!!!!!
Cho tam giác ABC có góc C:B:A=1:2:6
a) Tính góc C,B,C
b) Tia phân giác góc ngoài tại C cắt AB ở E. Tính AEC
Gíup mình với nhé! Mình cần gấp lắm rồi!!!!!!!#######
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC có góc B = 100o, góc C = 30o. Tia phân giác góc ngoài đỉnh A cắt đường thẳng BC tại E. Tính số đo góc AEB. Có nhận xét gì về tam giác AEB?
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 4 trang 137 SBT Toán 7 Tập 1
Bài tập 5 trang 137 SBT Toán 7 Tập 1
Bài tập 7 trang 137 SBT Toán 7 Tập 1
Bài tập 8 trang 138 SBT Toán 7 Tập 1
Bài tập 9 trang 138 SBT Toán 7 Tập 1
Bài tập 10 trang 138 SBT Toán 7 Tập 1
Bài tập 11 trang 138 SBT Toán 7 Tập 1
Bài tập 12 trang 138 SBT Toán 7 Tập 1
Bài tập 13 trang 138 SBT Toán 7 Tập 1
Bài tập 14 trang 138 SBT Toán 7 Tập 1
Bài tập 15 trang 138 SBT Toán 7 Tập 1
Bài tập 16 trang 139 SBT Toán 7 Tập 1
