Giải bài 9 tr 138 sách BT Toán lớp 7 Tập 1
Cho tam giác \(ABC\) vuông tại \(A.\) Kẻ \(AH\) vuông góc với \(BC\; (H ∈ BC)\). Tìm góc bằng góc \(B.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Trong tam giác vuông hai góc nhọn phụ nhau.
Lời giải chi tiết
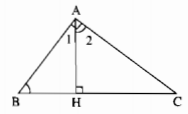
Có thể tìm góc B bằng hai cách:
*Cách 1
Ta có \(\widehat {{A_1}} + \widehat {{A_2}} = \widehat {BAC} = 90^\circ \) (1)
Vì ∆AHB vuông tại H nên:
\(\widehat B + \widehat A = 90^\circ \) (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: \(\widehat B = \widehat {{A_2}}\)
*Cách 2
Vì ∆ABC vuông tại A nên:
\(\widehat B + \widehat C = 90^\circ \) (tính chất tam giác vuông) (1)
Vì ∆AHC vuông tại H nên
\(\widehat {{A_2}} + \widehat C = 90^\circ \) (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: \(\widehat B = \widehat {{A_2}}\)
-- Mod Toán 7 HỌC247
-


Có hay không 1 tam giác mà 1 góc của nó bằng 60 độ và 2 góc kia đều nhỏ hơn 60 độ ?
bởi Mai Đào
 09/04/2019
09/04/2019
Có hay không một tam giác mà 1 góc của nó bằng 600 và:
a) 2 góc kia đều nhỏ hơn 600
b) 2 góc kia đều lớn hơn 600
c) 2 góc kia là 700 và 500
Theo dõi (0) 1 Trả lời -


1)Cho một điểm O nằm trong tam giác ABC
a)CM rằng BOC>BAC
b)Cho O là giao điểm của hai tia phân giác góc B và góc C. Hãy CM rằng BOC là góc tù.
2)Cho tam giác ABC có góc C hơn góc B \(90^{^{ }0}\). Kẻ đường cao AH.CM rằng góc BAH=ACH
3)Cho tam giác ABC có góc C kém góc B 90 độ.Kẻ phân giác của A cắt BC tại D. Tính góc ADB
4)Cho tam giác vuông ABC có hai góc nhọn B và C kém nhau 24 độ.Tính các góc ABC
5)Tính các góc của tam giác ABC biết Góc A-B=22độ;B-C=22độ
6)Tính số đo các gọc nhọn của tam giác ABC vuông tại A, biết phân giác BD của tam giác của góc Btaoj với AC góc BDC=110độ
7)CM rằng tổng 3 góc ngoài ở 3 đỉnh của một tam giác =360độ
Help me Tối mai 3/8 18:30 mik đi học rồi.Làm được bao nhiêu câu cũng được . Mik cảm ơn
Theo dõi (0) 1 Trả lời -


Tìm số đo x, y biết ABx=CAx=40 độ, ABC=70 độ
bởi Trần Phương Khanh
 09/04/2019
09/04/2019
Bài 1: Tìm số đo x; y:
a)
b)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A .
a) Tính số đo góc ABC , biết góc ACB= \(40^0\)
b) Vẽ tia phân giác của góc ABC cắt cạnh AC tại D . Trên tia BC lấy điểm E sao cho BE=BA . Chứng minh tam giác ABD = tam giác EBD .
c) Qua B vẽ đường thẳng xy vuông góc với AB . Từ A kẻ đường thẳng song song với BD cắt xy tại K . Chứng minh AK=BD
d) phần khó nhất ; Qua C vẽ đường thẳng vuông góc với BD tại H và cắt tia BA tại F . chứng minh ba điểm E;D;F thẳng hàng
bạn nào giải chi tiết mình sẽ tick ngay cảm ơn các bn nhiều
Theo dõi (0) 1 Trả lời -


Tính tổng góc B+C của tam giác ABC vuông tại A
bởi thúy ngọc
 22/02/2019
22/02/2019
cho tam giác ABC vuông tại a . tinh tong goc B +C
Theo dõi (0) 1 Trả lời -


Làm được bài này mới thực sự giỏi !
Cho \(\Delta ABC\) có \(\widehat{A}=180^0-3\widehat{C}\)
a ) Chứng minh : \(\widehat{B}=2\widehat{C}\)
b ) Từ một điểm D trên cạnh AB vẽ DE // BC ( \(E\in AC\)) . Hãy xác định điểm vị trí của điểm D đề ta Ed là tia phân giác góc \(\widehat{AEB}\)
Theo dõi (0) 1 Trả lời -


Chứng minh MK là phân giác của góc DMC biết phân giác của góc BAC cắt BC tại D
bởi Phan Thị Trinh
 22/02/2019
22/02/2019
Bài 1:Cho tam giác ABC,vẽ phân giác của góc BAC cắt BC tại D.Đường thẳng qua D song song với ABcắt AC tại M.Vẽ MK//AD. Chứng minh MK là phân giác của \(\widehat{DMC}\)
Help me @Akai Haruma @Phạm Hoàng Giang @Nguyễn Thanh Hằng @Bùi Thị Vân ....
Theo dõi (0) 1 Trả lời -


Tính số đo các góc của tam giác ABC biết 20A=15B=12C
bởi Thanh Nguyên
 22/02/2019
22/02/2019
(1)Cho tam giác ABC: góc A - góc B = góc B - góc C=10. Tính góc A,B,C
(2) Tính số đo của các góc của tam giác ABC, biết 20A=15B=12C
(3)Cho tam giác ABC có góc A=70; B-C=20. Tính góc B,C
(4)Cho tam giác ABC có góc B=80;C=40. Tia phân giác của góc B cắt ÁC tại D. Tính góc ADB
Theo dõi (0) 1 Trả lời -


Tính góc C ?
Theo dõi (0) 1 Trả lời -


Cho \(\Delta ABC\) có \(BC=4cm\). Trên tia đối của tia CB lấy điểm Q sao cho CQ = 3cm
a) Tính độ dài đoạn BQ
b) Biết \(\widehat{BAQ}=85^0,\widehat{BAC}=55^0\), tính \(\widehat{CAQ}\)
Theo dõi (0) 1 Trả lời -


Chứng minh AE=DC, AE vuông góc DC biết tam giác ABC nhọn, ở miền ngoài tam giác
bởi Nguyễn Phương Khanh
 10/04/2019
10/04/2019
Cho tam giác nhọn \(ABC\). Ở miền ngoài tam giác, lấy các điểm \(D,E\) sao cho \(\Delta ABD,\Delta CBE\) là các tam giác vuông cân đỉnh \(B\).Chứng minh \(AE=DC,AE\perp DC\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 7 trang 137 SBT Toán 7 Tập 1
Bài tập 8 trang 138 SBT Toán 7 Tập 1
Bài tập 10 trang 138 SBT Toán 7 Tập 1
Bài tập 11 trang 138 SBT Toán 7 Tập 1
Bài tập 12 trang 138 SBT Toán 7 Tập 1
Bài tập 13 trang 138 SBT Toán 7 Tập 1
Bài tập 14 trang 138 SBT Toán 7 Tập 1
Bài tập 15 trang 138 SBT Toán 7 Tập 1
Bài tập 16 trang 139 SBT Toán 7 Tập 1





