Bài tập 18 trang 139 SBT Toán 7 Tập 1

Hướng dẫn giải

- Góc ngoài tam giác bằng tổng hai góc trong không kề với góc đó.

- Tổng số đo hai góc kề bù bằng \(180^o\).

Lời giải chi tiết

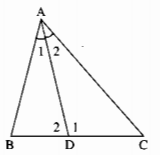
Trong ∆ABD ta có \(\widehat {{D_1}}\) là góc ngoài tại đỉnh D.

\(\widehat {{D_1}} = \widehat B + \widehat {{A_1}}\) (tính chất góc ngoài của tam giác)

Trong ∆ADC ta có \(\widehat {{D_2}}\) là góc ngoài tại đỉnh D

\(\widehat {{D_2}} = \widehat C + \widehat {{A_2}}\) (tínhchất góc ngoài của tam giác)

Ta có: \(\widehat B > \widehat C\left( {gt} \right);\widehat {{A_1}} = \widehat {{A_2}}\left( {gt} \right)\)

\( \Rightarrow \widehat {{D_1}} - \widehat {{D_2}} = \left( {\widehat B + \widehat {{A_1}}} \right) - \left( {\widehat C + \widehat {{A_2}}} \right)\)

\( = \widehat B - \widehat C = 20^\circ \)

\(\widehat {{D_1}} + \widehat {{D_2}} = 180^\circ \) (hai góc kề bù)

\(\eqalign{
& \Rightarrow \widehat {{D_1}} = \left( {180^\circ + 20^\circ } \right):2 = 100^\circ \cr
& \Rightarrow \widehat {{D_2}} = 100^\circ - 20^\circ = 80^\circ \cr} \)

Vậy \(\widehat {A{\rm{D}}C} = 100^\circ ;\widehat {A{\rm{D}}B} = 80^\circ \)

-- Mod Toán 7 HỌC247