Giải bài 12 tr 138 sách BT Toán lớp 7 Tập 1
Cho tam giác \(ABC.\) Các tia phân giác của các góc \(B\) và \(C\) cắt nhau ở \(I.\) Tính \(\widehat {BIC}\) biết rằng:
a) \({\rm{}}\widehat B = 80^\circ ,\widehat C = 40^\circ \)
b) \(\widehat A = 80^\circ \)
c) \(\widehat A = m^\circ \)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Định lí: Tổng ba góc của một tam giác bằng \({180^0}\)
Lời giải chi tiết
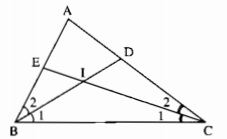
a) Ta có
\(\widehat {{B_1}} = {1 \over 2}\widehat {ABC} = {1 \over 2}.80^\circ = 40^\circ \) (vì BD là tia phân giác của \(\widehat {ABC}\))
\(\widehat {{C_1}} = {1 \over 2}\widehat {ACB} = {1 \over 2}.40^\circ = 20^\circ \) (vì CE là tia phân giác của \(\widehat {ACB}\))
Trong ∆IBC, ta có: \(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \) (tổng 3 góc trong tam giác)
\(\widehat {BIC} = 180^\circ - \left( {\widehat {\widehat {{B_1}} + {C_1}}} \right) = 180^\circ - \left( {40^\circ + 20^\circ } \right) = 120^\circ \)
b) Ta có:
\(\widehat {{B_1}} = {1 \over 2}\widehat B\) (vì BD là tia phân giác \(\widehat B\))
\(\widehat {{C_1}} = {1 \over 2}\widehat C\) (vì CE là tia phân giác \(\widehat C\))
Trong ∆ABC, ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong tam giác)
Suy ra \(\widehat B + \widehat C = 180^\circ - \widehat A = 180^\circ - 80^\circ = 100^\circ \)
Trong ∆IBC, ta có: \(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \)
Vậy \(\widehat {BIC} = 180^\circ - \left( {\widehat {{B_1}} + \widehat {{C_1}}} \right) = 180^\circ - {{\widehat B + \widehat C} \over 2} = 180^\circ - {{100^\circ } \over 2} = 130^\circ \)
c) Ta có: \(\widehat B + \widehat C = 180 - m^\circ \)
Vậy \(\widehat {BIC} = 180^\circ - {{180^\circ - m^\circ } \over 2} = 180^\circ - 90^\circ + {{m^\circ } \over 2} = 90^\circ + {{m^\circ } \over 2}\)
-- Mod Toán 7 HỌC247
-
BÀI 6 : Cho tam giác ABC cân ; góc BAC = góc BCA = 80 độ .Từ đỉnh A và C vẽ 2 đường thẳng cắt các cạnh đối theo thứ tự tại D và E sao cho : góc CAD = 60 độ ; góc ACE = 50 độ .Tính góc ADE .?
Theo dõi (0) 1 Trả lời -
Trong một tam giác, góc nhỏ nhất là góc nhọn ?
bởi Nguyễn Hồng Tiến
25/04/2019
Chọn câu đúng, câu sai
1.trong một tam giác, góc nhỏ nhất là góc nhọn
2.Trong một tam giác, có ít nhất là hai góc nhọn
3.Trong một tam giác, góc lớn nhất là góc tù
4.Trong một tam giác vuông,, 2 góc nhọn bù nhau
5.Nếu góc A là góc ở đáy của một tam giác cân thì góc A < 90 độ
6. Nếu góc A là góc ở đỉnh của một tam giác cân thì góc A < 90 độ
Theo dõi (0) 1 Trả lời -
Tính số đo góc ADE biết tam giác ABC vuông tại A có B=56 độ, trên cạnh AC lấy điểm D
bởi thanh hằng
26/04/2019
Cho ΔABC vuông tại A có B =56 độ. Trên cạnh AC lấy điểm D, từ D kẻ DE vuông góc với BO (E ϵ BC) Số đo góc ADE là ...
Theo dõi (0) 1 Trả lời -
Tính tổng số đo 3 góc ngoài của 1 tam giác
bởi thu hằng
26/04/2019
trong 1 tam giác tổng số đo 3 góc ngoài là
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC cân tại A . Lấy điểm M thuộc cạnh AB , lấy điểm N thuộc cạnh AC sao cho BM=CN .
a) Chứng minh tam giác AMN là tam giác cân
b) Cho góc B = 50 độ , tính góc ANM
c) Chứng minh MN song song với BC .
Theo dõi (0) 1 Trả lời -
Tính góc AIB biết tam giác ABC cân tại B có góc ABC=80 độ, IAC=10 độ, ICA=30 độ
bởi hành thư
08/05/2019
cho tam giac ABC cân tai B, có góc ABC= 80o . I là 1 điểm nằm tron tam giac, biết góc IAC= 10o ,ICA=30o
tính góc AIB
Theo dõi (0) 1 Trả lời -
Tính góc ABC trong từng trường hợp biết kèo hợp với nhau 1 góc bằng 145 độ nếu mái là tôn
bởi Lê Chí Thiện
08/05/2019
rong xây dựng, hai thanh AB và AC của vì kèo một mái nhà thường bằng nhau và thường tạo với nhau một góc bằng:
a) 145 độ nếu mái là tôn
b) 100 độ nếu là mái ngói
Tính góc ABC trong từng trường hợp trênTheo dõi (0) 1 Trả lời -
Chứng minh BM vuông góc CM biết tam giác ABC có góc A < 90 độ, tam giác ABM và CAN vuông cân tại A
bởi Nguyễn Thị Trang
08/05/2019
cho tam giác ABC có góc  < 90 độ. Vẽ ra ngoài tam giác ABC các tam giác vuông cân tại A là tam giác ABM và tam giác CAN. Chứng minh
a) tam giác AMC = tam giác ANB
b)BN vuông góc với CM
Theo dõi (0) 1 Trả lời -
Tính số đo góc ACB biết tam giác ABC vuông tại A, AH vuông góc BC tại H và góc BAH=35 độ
bởi thúy ngọc
08/05/2019
Cho tam giác ABC vuông tại A.Kẻ AH vuông góc với BC tại H.Biết góc BAH=35o.Tìm số đo góc ACB
Theo dõi (0) 1 Trả lời -
Bài 1.1 trang 139 sách bài tập toán 7 tập 1
bởi thùy trang
28/09/2018
Bài 1.1 - Bài tập bổ sung (Sách bài tập - tập 1 - trang 139)Tam giác ABC có \(\widehat{A}=40^0\). Các tia phân giác của các góc B và C cắt nhau ở I. Góc BIC bằng :
(A) \(40^0\) (B) \(70^0\) (C) \(110^0\) (D) \(140^0\)
Hãy chọn phương án đúng ?
Theo dõi (0) 3 Trả lời -
Bài 18* (Sách bài tập - tập 1 - trang 139)
Cho tam giác ABC có \(\widehat{B}-\widehat{C}=20^0\). Tia phân giác của góc A cắt BC ở D.
Tính số đo các góc \(\widehat{ADC},\widehat{ADB}\) ?
Theo dõi (0) 1 Trả lời
