Giải bài 16 tr 139 sách BT Toán lớp 7 Tập 1
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ \), kẻ \(AH\) vuông góc với \(BC\; (H ∈ BC).\) Các tia phân giác của các góc \(\widehat C\) và \(\widehat {BAH}\) cắt nhau ở \(I\). Chứng minh rằng: \(\widehat {AIC} = 90^\circ \)
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Định lí: Tổng ba góc của một tam giác bằng \({180^o}\)
- Trong tam giác vuông hai góc nhọn phụ nhau.
Lời giải chi tiết
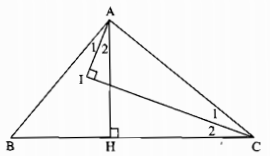
Ta có: \(AH \bot BC\left( {gt} \right) \Rightarrow \Delta AHB\) vuông tại H
Trong tam giác vuông AHB ta có: \(\widehat {AHB} = 90^\circ \)
\( \Rightarrow \widehat B + \widehat {BAH} = 90^\circ \left( 1 \right)\)
Trong tam giác vuông ABC, ta có: \(\widehat {BAC} = 90^\circ \)
\( \Rightarrow \widehat B + \widehat C = 90^\circ \left( 2 \right)\)
Từ (1) và (2) suy ra: \(\widehat {BAH} = \widehat C\)
\(\eqalign{
& \widehat {{A_1}} = \widehat {{A_2}} = {1 \over 2}\widehat {BAH}\left( {gt} \right) \cr
& \widehat {{C_1}} = \widehat {{C_2}} = {1 \over 2}\widehat C\left( {gt} \right) \cr} \)
Suy ra: \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{C_1}} = \widehat {{C_2}}\)
\(\widehat {{A_1}} + \widehat {IAC} = \widehat {BAC} = 90^\circ \)
Suy ra: \(\widehat {{C_1}} + \widehat {IAC} = 90^\circ \)
Trong ∆ AIC ta có: \(\widehat {IAC} + \widehat {{C_1}} = 90^\circ \)
Vậy \(\widehat {AIC} = 90^\circ \)
-- Mod Toán 7 HỌC247
-


Chứng minh MN song song với BC biết tam giác ABC đều
bởi Việt Long
 19/12/2019
19/12/2019
cho tam giac ABC deu tren cac canh AB va AC lan luot lay cac diem M va N sao cho AM=AN chung minh tam giac AMN la tam giac deu b) MN song song voi BC
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác MAD = tam giác MCE biết tam giác ABC cân có M là trung điểm của BC
bởi Lê Vinh
 19/12/2019
19/12/2019
cho tam giác ABCcân ( AB=AC) .Trên các cạch AB và AC lấy tương ứng 2 điểm D và E sao cho AD =AE .Gọi M là trung điểm của BC . chứng minh
a) DE //BC
B) tam giác MAD = tam giác MCE
c) chứng minh AMD= tam giác AME
GIÚP MK NHA M.N HUHU..................................CẦN GẤP LẮM
Theo dõi (0) 1 Trả lời -


Tính số đo các góc của tam giác AMN biết tam giác ABC có góc A=80 độ, góc B=60 độ
bởi minh thuận
 19/12/2019
19/12/2019
Cho tam giac ABC co \(\widehat{A}\)=80, \(\widehat{B}\)=60. Tren tia doi BC lay diem M, tren tia doi cua CB lay diem N sao cho BM=BA, CN=CA. Tinh so do cac goc cua tam giac AMN
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A , đường cao AH .Biết B= 38 độ. tìm HAC=.......độ
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có A - B = 20O ; B - C = 20O
Tính góc C
Theo dõi (0) 1 Trả lời -


Cho \(\Delta ABC\) có \(\widehat{A}=60^0\); \(\widehat{H}=50^0\). Tia phân giác của góc K cắt EK tại D . Tính \(\widehat{EDK};\widehat{HDK}\)
Theo dõi (0) 1 Trả lời -


giup mik voi mk cần gấp
Cho tam giác ABC vuông tại A có AB<AC. Trên cạnh BC lấy điểm D sao cho BD = BA kẻ AH vuông góc BC; DK vuông góc AC
a) CM góc C= góc HAB
b) CM Ak là phân giác góc HAC
c) CM AK= AH và AD là đường trung trực HK
d) CM AB=AC<BC+AH
Theo dõi (0) 1 Trả lời -


Cho góc xOy bằng 60 độ và điểm A nằm trong góc xOy.vẽ điểm b sao cho oy là đường trung trực của AB. Vẽ điểm C sao cho Oy là đường trung trực của AC .Chứng minh rằng
a,OB = BC
b,Tính số đo góc BOC
Theo dõi (0) 1 Trả lời -


Bài tập 1: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC. Gọi giao điểm của đường thẳng này với AB,AC theo thứ tự là D,E. Chứng minh rằng DE = BD + CE.
Bài tập 2: Cho đường tròn tâm O đường kính AB. Gọi M là một điểm nằm trên đường tròn. Tính số đo góc AMB.
Theo dõi (0) 1 Trả lời -


Số đo độ của góc BIC trong tam giác ABC có góc A bằng 40 độ và I là giao điểm của các phân giác trong BD; CE?
bởi hi hi
 19/12/2019
19/12/2019
Số đo độ của góc BIC trong tam giác ABC có góc A bằng 40 độ và I là giao điểm của các phân giác trong BD; CE.......giải giúp mk với????????????
Theo dõi (0) 2 Trả lời -


Chứng minh tam giác ABC vuông biết tia phân giác của góc B và góc C cắt nhau tại I và BIC = 135 độ
bởi Cam Ngan
 23/12/2019
23/12/2019
cho tam giác abc, tia phân giác của góc B và góc C cắt nhau tại I, biết BIC = 135 độ. Chứng minh ABC vuông
Theo dõi (0) 1 Trả lời





