Giải bài 15 tr 138 sách BT Toán lớp 7 Tập 1
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ \). Gọi \(E\) là một điểm nằm trong tam giác đó. Chứng minh rằng góc \(BEC\) là góc tù.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Góc ngoài tam giác lớn hơn hai góc trong không kề với góc đó.
Lời giải chi tiết
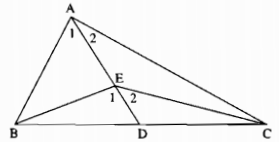
Kéo dài AE cắt BC tại D.
Trong ∆ABE ta có \(\widehat {{E_1}}\) là góc ngoài tại đỉnh E
Suy ra: \(\widehat {{E_1}} > \widehat {{A_1}}\) (tính chất góc ngoài của tam giác) (1)
Trong ∆AEC ta có \(\widehat {{E_2}}\) là góc ngoài tại đỉnh E
Suy ra: \(\widehat {{E_2}} > \widehat {{A_2}}\) (tính chất góc ngoài của tam giác) (2)
Cộng từng vế (1) và (2) ra có:
\(\widehat {{E_1}} + \widehat {{E_2}} > \widehat {{A_1}} + \widehat {{A_2}}\)
Hay \(\widehat {BEC} > \widehat {BAC} = 90^\circ \)
Vậy \(\widehat {BEC}\) là góc tù
-- Mod Toán 7 HỌC247
-


tam giác ABC có góc A= 30\(^0\) , góc B = 70\(^o\). tính số đo góc C
tam giác ABC vuông góc tại A, có góc C = 40\(^o\). tính số đo gócB?
Theo dõi (0) 1 Trả lời -


Tính góc C biết tam giác ABC cân tại A có góc A=80 độ
bởi thu phương
 17/12/2019
17/12/2019
cho \(\Delta\) ABC cân tại A góc A=80 góc C = ?
Theo dõi (0) 1 Trả lời -


tam giác ABC có góc B>góc C. đường phân giác góc ngoài đỉnh A cắt BC tại E, góc A=60, góc AEB=15 . vậy góc C=?
Theo dõi (0) 1 Trả lời -


1) Cho tam giác ABC vuông tại A . Biết AB + AC = 49 cm ; AB - AC = 7 cm . Tính cạnh BC
2) Cho tam giác ABC vuông tại A ( AB < AC ) , phân giác AD . Từ D kẻ đường thẳng vuông góc với BC cắt AC tại M . Tính góc MBC
3) Tam giác ABC có góc B = 45 * ; góc A = 15* . Trên tia đối tia CB lấy điểm D sao cho CD = 2BC. Tính góc ADBTheo dõi (0) 1 Trả lời -


cho \(\Delta ABC\left(\widehat{A}=90^o\right)\) , kẻ \(AH\perp BC\left(H\in BC\right)\) trên đường thẳng \(\perp BC\) tại B , lấy D khong cùng nửa mặt phẳng bờ BC đối với A
a) \(\Delta AHB=\Delta DBH\)
b) DB//DH
c) tính \(\widehat{ACB}\) biết \(\widehat{BAH}=35^o\)
Theo dõi (0) 1 Trả lời -


Tìm số đo góc còn lại biết rằng góc B=2lần góc C
bởi Anh Trần
 17/12/2019
17/12/2019
Giúp mik vs nhé
Cho tam giác ABC có Góc A=90độ.Tìm Số Đo góc còn lại biết rằng góc B=2lần góc C
giúp với
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A có B=600. Vẽ AH vuông góc vs BC tại H
a) Tính số đo góc HAB
b) Trên cạnh AC lấy điểm D sao cho AD=AH. Gọi I là trung điểm của cạnh HD. Chứng minh tam giác AHI và tam giác ADI
c) Tia AI cắt cạnh HC tại điểm K. Chứng minh tam giác AHK = tam giác ADK từ đó suy ra AB// KD
d) Trên tia đối của tia HA lấy điểm E sao cho HE=AH. Chứng minh H là trung điểm của BK và 3 điểm D,K,E thẳng hàng
Theo dõi (0) 1 Trả lời -


1. Cho tam giác ABC có góc B=50 độ. Từ A kẻ đường thẳng \\ vs BC cắt tia p/g của góc B ở E.
a) CM: ΔAEB là tam giác cân.
b) Tính góc BAE
2. cho tam giác ABC cân tại A. Trên cạnh AB và AC lấy tương ứng 2 điểm D và E sao cho AD= AE. Gọi M là trung điểm của BC. CMR:
a) DE\\BC
b) ΔMBD=ΔMCE
c)ΔAMD=ΔAME.
3.Cho tam giác ABC cân tại A. Gọi Am là tia phân giác góc ngoài tại đỉnh A của tam giác đó. CM Am\\BC.
4. Cho tam giác đều ABC. Trên tia đối của các tia AB,BC,CA lấy theo thứ tự ba điểm D,E,F sao cho AD=BE=CF. CM ΔDEF là tam giác đều.
( GIÚP MÌNH VỚI NHÉ!!! VẼ HÌNH VÀ TRÌNH BÀY CHI TIẾT NHÉ! MÌNH ĐANG CẦN GẤP! THANKS!!! ^_^)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có AB= AC, M là trung điểm của BC. Trên tia đối cả tia MA lấy điểm d sao cho: AM= MD
a) Chứng minh tam giác AMB= tam giác DMC
b) Chứng minh AB song song với DC
c) Chứng minh AM vuông góc với BC
d) Tìm điều kiện của tam giác ABC để góc ADC=30 độ
Theo dõi (0) 1 Trả lời -


Tính góc B, góc C của tam giác ABC biết tam giác ABC vuông ở A và BC = 2AB
bởi Nguyễn Lệ Diễm
 19/12/2019
19/12/2019
Cho tam giác ABC vuông ở A và BC = 2.AB. Gọi E là trung điểm của BC. Tia phân giác của góc B cắt AC tại D.
a) Chứng minh DB là phân giác của góc ADE.
b) Chứng minh BD = DC.
c) Tính góc B, góc C của tam giác ABC
Theo dõi (0) 1 Trả lời -


Tính góc B và C biết tam giác ABC có góc A=75 độ và C=2B
bởi Lan Anh
 19/12/2019
19/12/2019
Cho Δ ABC có góc A = 75 độ.Tính góc B và C,biết:
a, C= 2B
b, C- B= 25
Theo dõi (0) 1 Trả lời






