Giải bài 14 tr 138 sách BT Toán lớp 7 Tập 1
Chứng minh rằng tổng ba góc ngoài ở ba đỉnh của một tam giác thì bằng \(360^\circ \).
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Định lí: Tổng ba góc của một tam giác bằng \({180^o}\).
- Tổng số đo hai góc kề bù bằng \(180^o\).
Lời giải chi tiết
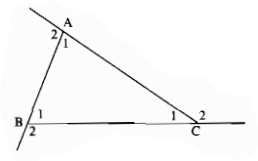
Ta có: \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (hai góc kề bù)
\(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) (hai góc kề bù)
\(\widehat {{C_1}} + \widehat {{C_2}} = 180^\circ \) (hai góc kề bù)
Suy ra: \(\widehat {{A_1}} + \widehat {{A_2}} + \widehat {{B_1}} + \widehat {{B_2}} + \widehat {{C_1}} + \widehat {{C_2}} = 180^\circ .3 = 540^\circ \)
\( \Rightarrow \widehat {{A_2}} + \widehat {{B_2}} + \widehat {{C_2}} = 540^\circ - \left( {\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}}} \right)\left( 1 \right)\)
Trong ∆ABC ta có:
\(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \) (tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra:
\(\widehat {{A_2}} + \widehat {{B_2}} + \widehat {{C_2}} = 540^\circ - 180^\circ = 360^\circ \)
-- Mod Toán 7 HỌC247
-


Tính chất góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó suy ra từ định lí nào?
bởi Lê Nhi
 11/12/2019
11/12/2019
-Các tính chất sau đây được suy ra trục tiếp từ định lí nào?
i)Góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.
ii) Trong một tam giác vuông, hai góc nhọn phụ nhau.
iii)Trong một tam giác đều,hai góc nhọn phụ nhau.
iv)Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
-Cho điểm  nằm ngoài đường thẳng a. Vẽ cung tròn tâm  cắt đường thẳng a ở B và C. Vẽ các cung tròn tâm B và tâm Ccó cùng bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi điểm đó là D. Hãy giải thích vì sao AD vuông góc với đường thẳng a.
Theo dõi (0) 1 Trả lời -


Trong một tam giác, góc nhỏ nhất là góc nhọn?
bởi Lê Tấn Vũ
 11/12/2019
11/12/2019
Câu Đúng Sai 1.Trong một tam giác, góc nhỏ nhất là góc nhọn.
2.Trong một tam giác, có ít nhất là hai góc nhọn.
3.Trong một tam giác, góc lớn nhất là góc tù.
4. Trong một tam giác vuông, hai góc nhọn bù nhau.
5.Nếu  là góc ở đáy của một tam giác cân thì  < 90o.
6.Nếu  là góc ở đỉnh của một tam giác cân thì Â> 90o.
Theo dõi (0) 1 Trả lời -


Số đo góc C bằng bao nhiêu biết tam giác ABC vuông tại A có số đo góc B = 40 độ?
bởi Tram Anh
 12/12/2019
12/12/2019
1. Cho tam giác ABC vuông tại A , biết số đo góc B = 40 độ . Số đo góc C = bao nhiêu ?
2. Cho tam giác DEF cân tại D , biết số đo góc E = 50 độ . Số đo góc D = bao nhiêu ?
3. Đánh dấu " X " vào câu trả lời đúng :
Câu Đúng Sai A. Tam giác cân có 1 góc = 60 độ là tam giác đều.
B. Góc ngoài của 1 tam giác lớn hơn 1 góc trong không kề với nó
4. Tam giác ABC có góc A = 90 độ ; góc B = 45 độ thì tam giác ABC là tam giác gì ?
5. Trong 1 tam giác cân có góc đỉnh = 110 độ . Mỗi góc ở đáy sẽ có số đo là bao nhiêu ?
6. Trong tam giác ABC có AB = 4cm , AC = 5cm , BC = 3cm có thể kết luận : tam giác ABC
A. Vuông tại C
B. Cân
C. Vuông tại B
D. Đều
7. Tam giác cân muốn trở thành tam giác đều thì cần có số đo của 1 góc là bao nhiêu ?
8. Tam giác ABC vuông tại A , kết luận nào đúng ?
A. \(AB^2=BC^2+AC^2\)
B. \(BC^2=AB^2+AC^2\)
C. \(AC^2=AB^2-BC^2\)
D. \(BC^2=AB^2-AC^2\)
9. Trong các tam giác có số đo lần lượt như sau , bộ ba số đo nào cho ta tam giác vuông ?
A. 3,5,7 ( cm )
B. 6,8,9 ( cm )
C. 5,12,13 ( cm )
D. 10,10,100 ( cm )
10. Góc ngoài của 1 tam giác luôn = :
A. Tổng 3 góc trong không kề vs nó
B. Tổng 2 góc trong kề vs nó
C. Tổng 2 góc trong không kề với nó
D. = với góc trong kề vs nó
Theo dõi (0) 1 Trả lời -


Tính số đo góc A của tam giác ABC biết \(\widehat{A}-\widehat{B}=22^o;\widehat{B}-\widehat{C}=22^o\)
Theo dõi (0) 1 Trả lời -


Chứng minh góc BOC=góc A+góc ABO+góc ACO biết O là điểm nằm trong tam giác ABC
bởi Mai Đào
 12/12/2019
12/12/2019
cho \(\Delta ABC\) ,O là điểm nằm trong tam giác.CM:
a) \(\widehat{BOC}=\widehat{A}+\widehat{ABO}+\widehat{ACO}\)
b) Biết \(\widehat{ABO}+\widehat{ACO}=90^o-\dfrac{\widehat{A}}{2}\) và BO là tia phân giác \(\widehat{B}\) .CM: CO là tia phân giác \(\widehat{C}\)
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABC vẽ trên giấy kẻ ô vuông như hình 121 là tam giác nhọn
bởi cuc trang
 16/12/2019
16/12/2019
Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông như hình 121 là tam giác nhọn ( tức là tam giác có cả ba góc đều là góc nhọn )
có bạn nào học vnen thì cho mik hỏi! bài này ở trang 173 sách toán tập một ạ
Theo dõi (0) 1 Trả lời -


Tính góc A của tam giác ABC biết A+B=C, 2A=3B
bởi thuy linh
 16/12/2019
16/12/2019
Tính góc A của \(\bigtriangleup\)ABC biết: \(\widehat{A} \) + \(\widehat{B} \) = \(\widehat{C} \); 2\(\widehat{A} \) = 3\(\widehat{B} \)
Theo dõi (0) 1 Trả lời -


cho tam giac MNP co goc M=500, N-P=400. Tinh so do goc N va goc P
Theo dõi (0) 1 Trả lời -


Tính số đo góc A biết trong tam giác ABC các tia phân giác của góc B và góc C cắt nhau tại G
bởi Phạm Phú Lộc Nữ
 17/12/2019
17/12/2019
Trong tam giác ABC,các tia phân giác của \(\widehat{B}\) và \(\widehat{C}\) cắt nhau tại G.Nếu \(\widehat{BGC}\) = 130o thì số đo góc A là...
Theo dõi (0) 1 Trả lời -


Tính số đo góc C biết hai đường ngoài đỉnh A và đỉnh B cắt nhau tại J tạo thành góc AJB bằng 50 độ
bởi Nguyễn Trung Thành
 17/12/2019
17/12/2019
Cho tam giác ABC. Hai đường ngoài đỉnh A và đỉnh B cắt nhau tại J tạo thành góc AJB bằng 50o. Vậy số đo góc C bằng:
Theo dõi (0) 1 Trả lời -


Chứng minh bất đẳng thức tam giác
bởi Thùy Nguyễn
 24/10/2018
24/10/2018
a) tìm một cách chứng minh khác của bất đẳng thức tam giác
b)cho tam giác MNP.Gọi I là trung điểm của đoạn thẳng MN. Chứng minh rằng: PM+PN>2PI
Theo dõi (0) 1 Trả lời







