Giải bài 6 tr 58 sách GK Toán ĐS & GT lớp 11
Chứng minh rằng:
a) \(\small 11^{10} - 1\) chia hết cho 100;
b) \(\small 101^{100} - 1\) chia hết cho 10 000;
c) \(\small \sqrt{10}[(1+\sqrt{10})^{100}-(1-\sqrt{10})^{100}]\) là một số nguyên.
Hướng dẫn giải chi tiết bài 6
Câu a:
Ta có:
\(11^{10}- 1 = (1 + 10)^{10} =C_{10}^{0}.10^{10}+C_{10}^{1}.10^9+...\)\(+ C_{10}^{8}.10^2+C_{10}^{9}.10+C_{10}^{10}\)
\(=100(C_{10}^{0}.10^8+C_{10}^{1}.10^7+...+ C_{10}^{8}+1)+1\)
Tổng sau cùng chia hết cho 100 suy ra 1110 – 1 chia hết cho 100.
Câu b:
Ta có \(101^{100}=(100+1)^{100}=C_{100}^{0}.100^{100}\)
\(+C_{100}^{1}.100^{99}+...+ C_{100}^{99}.100+C_{100}^{100}\)
\(=100^2\left [ C_{100}^{0}.100^{98}+C_{100}^{1}.100^{97}+...+1 \right ]\)
Vậy \(101^{100}=10000\left [ C_{100}^{0}.100^{98}+C_{100}^{1}.100^{97}+...+1 \right ]\) chia hết cho 10 000.
Câu c:
Ta có \((1+\sqrt{10})^{100}=C_{100}^{0}+C_{100}^{1}\sqrt{10}+C_{100}^{2}\sqrt{10^2}+...+\)\(C_{100}^{99}\sqrt{10^{99}}+C_{100}^{100}\)
\((1-\sqrt{10})^{100}=C_{100}^{0}+C_{100}^{1}\sqrt{10}+C_{100}^{2}\sqrt{10^2}+...-\)\(C_{100}^{99}\sqrt{10^{99}}+C_{100}^{100}\)
Do đó: \((1+\sqrt{10})^{100}-(1-\sqrt{10})^{100}=2 \left ( C_{100}^{0}+C_{100}^{1}\sqrt{10}+C_{100}^{2}\sqrt{10^2}+...+ C_{100}^{99}\sqrt{10^{99}}\right )\)
Vậy nên: \(\sqrt{40}\left [ (1+\sqrt{10})^{100}-(1-\sqrt{10})^{100} \right ].\)
-- Mod Toán 11 HỌC247
-

 Câu tính tổng
Câu tính tổng Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tìm n dương thỏa C_n^2-n=9
bởi Ngọc Mai
 21/12/2019
Tìm n
21/12/2019
Tìm n Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Số hạng không chứa x trong khai triển
Số hạng không chứa x trong khai triển Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -

 Trong khai triển nhị thức (2a-b)^5 hệ số của số hạng thứ 3 làTheo dõi (0) 4 Trả lời
Trong khai triển nhị thức (2a-b)^5 hệ số của số hạng thứ 3 làTheo dõi (0) 4 Trả lời -

 Câu 34
Câu 34 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Số hạng thứ sáu trong khai triển(3x^2-y)^10 là?
bởi Thu Hồng
 17/12/2019
Làm ơn giúp tôi
17/12/2019
Làm ơn giúp tôi Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính tổng 1×3^0×5^n-1
bởi Linh Mai
 16/12/2019
Giải dùm vsTheo dõi (0) 0 Trả lời
16/12/2019
Giải dùm vsTheo dõi (0) 0 Trả lời -


Tìm hệ số x^7 trong khai triển (x-2)^4(x-1)^5
bởi Minh Thư
 16/12/2019
16/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm hệ số x^6 trong khai triển (1/x+x^3)^10
bởi Nhựt Nguyễn
 13/12/2019
Giải
13/12/2019
Giải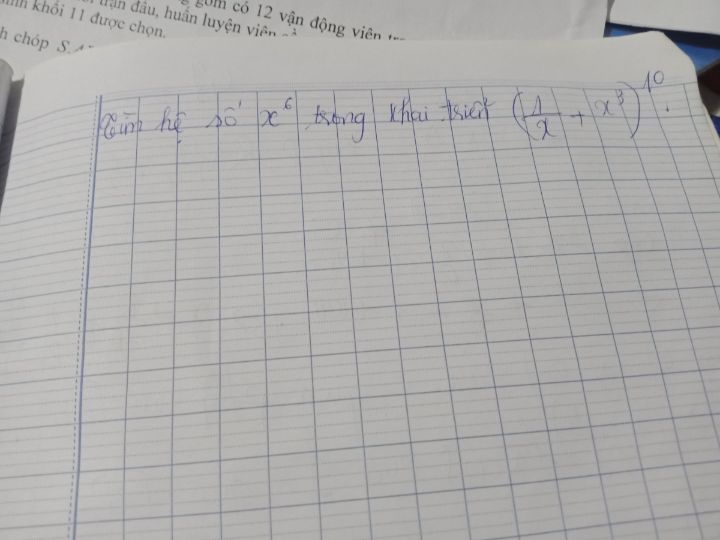 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 4 trang 58 SGK Đại số & Giải tích 11
Bài tập 5 trang 58 SGK Đại số & Giải tích 11
Bài tập 2.32 trang 79 SBT Toán 11
Bài tập 2.33 trang 79 SBT Toán 11
Bài tập 2.34 trang 79 SBT Toán 11
Bài tập 2.35 trang 79 SBT Toán 11
Bài tập 2.36 trang 79 SBT Toán 11
Bài tập 2.37 trang 79 SBT Toán 11
Bài tập 2.38 trang 79 SBT Toán 11
Bài tập 2.39 trang 79 SBT Toán 11
Bài tập 17 trang 67 SGK Toán 11 NC
Bài tập 18 trang 67 SGK Toán 11 NC
Bài tập 19 trang 67 SGK Toán 11 NC
Bài tập 20 trang 67 SGK Toán 11 NC
Bài tập 21 trang 67 SGK Toán 11 NC
Bài tập 22 trang 67 SGK Toán 11 NC





