Giải bài 2.35 tr 79 SBT Toán 11
Trong khai triển của (x+a)3(x−b)6, hệ số của x7 là −9 và không có số hạng chứa x8. Tìm a và b.
Hướng dẫn giải chi tiết
Ta có \({\left( {x + a} \right)^3}{\left( {x - b} \right)^6} = \mathop \sum \limits_{m = 0}^3 C_3^m{x^{3 - m}}{a^m}\mathop \sum \limits_{n = 0}^6 C_6^n{x^{6 - n}}{( - b)^n}\)
\(\begin{array}{l}
= \left( {C_3^0{x^3} + C_3^1{x^2}a + C_3^2x{a^2} + C_3^3{a^3}} \right)[C_6^0{x^6} + C_6^1{x^5}( - b) + C_6^2{x^4}{( - b)^2} + C_6^3{x^3}{( - b)^3} + C_6^4{x^2}{( - b)^4} + C_6^5x{( - b)^5}\\
+ C_6^6{( - b)^6}]
\end{array}\)
Số hạng chứa x7 là \([C_3^0.C_6^2{( - b)^2} + C_3^1a.C_6^1( - b) + C_3^2{a^2}C_6^0]{x^7}\)
Số hạng chứa x8 là \(\left[ {C_3^0.C_6^1\left( { - b} \right) + C_3^1a.C_6^0} \right]{x^8}\)
Theo bài ra ta có
\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{15{b^2} - 18ab + 3{a^2} = - 9}\\
{ - 6b + 3a = 0}
\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{a = 2b}\\
{{b^2} = 1}
\end{array}} \right.\\
\Rightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
a = 2,\\
b = 1
\end{array} \right.\\
\left\{ \begin{array}{l}
a = - 2\\
b = - 1
\end{array} \right.
\end{array} \right.
\end{array}\)
-- Mod Toán 11 HỌC247
-

 Tìm số hạng chứa x^10trong khai triển (3x^3-2/x^2)^5Theo dõi (0) 5 Trả lời
Tìm số hạng chứa x^10trong khai triển (3x^3-2/x^2)^5Theo dõi (0) 5 Trả lời -


Trong khai triển (2x-1)^10, hệ số chứa x^8 là?
bởi Đặng Na
 10/11/2019
Trong khai triển (2x-1)^10, hệ số chứa x^8 làTheo dõi (0) 2 Trả lời
10/11/2019
Trong khai triển (2x-1)^10, hệ số chứa x^8 làTheo dõi (0) 2 Trả lời -


 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Khai triển nhị thức Niu tơn (x-1/x) ^7
bởi Ngọc Nguyễn Thị Hồng
 07/11/2019
(x-1/x) ^7=??Theo dõi (1) 3 Trả lời
07/11/2019
(x-1/x) ^7=??Theo dõi (1) 3 Trả lời -

 Mọi người giúp em với ạ
Mọi người giúp em với ạ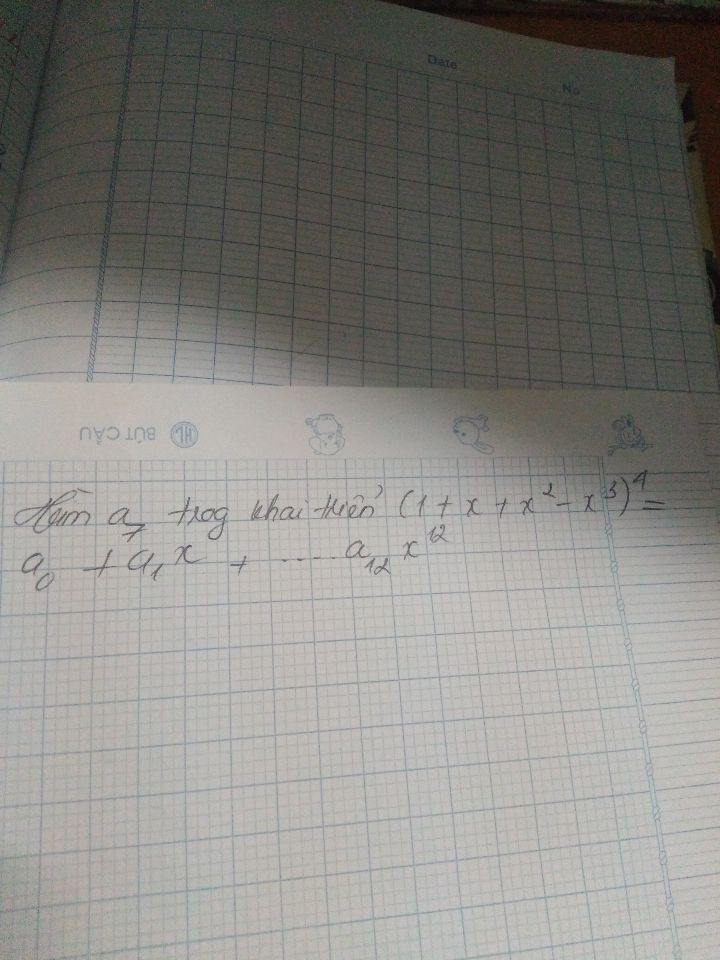 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Khai triển (2x-x^2)^10
bởi vũ hải triều
 07/11/2019
(2x-x^2)^10Theo dõi (0) 2 Trả lời
07/11/2019
(2x-x^2)^10Theo dõi (0) 2 Trả lời -


Khai triển (x^2-1/2)^6
bởi Minh Anh
 06/11/2019
(x^2-1/2)^6Theo dõi (0) 1 Trả lời
06/11/2019
(x^2-1/2)^6Theo dõi (0) 1 Trả lời -


Tìm số nguyên dương bé nhất sao cho trong khai triển (1+x)^2 có hai hệ số liên tiếp có tỉ số là 7/15
bởi Tiếu Ninh Hinh
 01/11/2019
Tìm số nguyên dương bé nhất sao cho trong khai triển ( 1 x )^2 có hai hệ số liên tiếp có tỉ số là 7/15.Theo dõi (0) 1 Trả lời
01/11/2019
Tìm số nguyên dương bé nhất sao cho trong khai triển ( 1 x )^2 có hai hệ số liên tiếp có tỉ số là 7/15.Theo dõi (0) 1 Trả lời -

 Khai triển (a-2b) ^8 hệ số dang chứa a^4.b4Theo dõi (0) 5 Trả lời
Khai triển (a-2b) ^8 hệ số dang chứa a^4.b4Theo dõi (0) 5 Trả lời
Bài tập SGK khác
Bài tập 2.33 trang 79 SBT Toán 11
Bài tập 2.34 trang 79 SBT Toán 11
Bài tập 2.36 trang 79 SBT Toán 11
Bài tập 2.37 trang 79 SBT Toán 11
Bài tập 2.38 trang 79 SBT Toán 11
Bài tập 2.39 trang 79 SBT Toán 11
Bài tập 17 trang 67 SGK Toán 11 NC
Bài tập 18 trang 67 SGK Toán 11 NC
Bài tập 19 trang 67 SGK Toán 11 NC
Bài tập 20 trang 67 SGK Toán 11 NC
Bài tập 21 trang 67 SGK Toán 11 NC
Bài tập 22 trang 67 SGK Toán 11 NC





