Giải bài 2.33 tr 79 SBT Toán 11
Viết khai triển của (1+x)6.
a) Dùng ba số hạng đầu để tính gần đúng 1,016.
b) Dùng máy tính để kiểm tra kết quả trên.
Hướng dẫn giải chi tiết
Ta có:
\(\begin{array}{l}
{(1 + x)^6} = \mathop \sum \limits_{k = 0}^6 C_6^k{x^k} = C_6^0{x^0} + C_6^1{x^1} + C_6^2{x^2} + C_6^3{x^3} + C_6^4{x^4} + C_6^5{x^5} + C_6^6{x^6}\\
= 1 + 6x + 15{x^2} + 20{x^3} + 15x4 + 6x5 + x6
\end{array}\)
a) Ta có khai triển: \({\left( {1 + x} \right)^6} = 1 + 6x + 15{x^2} + 20{x^3} + 15{x^4} + 6{x^5} + {x^6}\)
Nên \(1,{01^6} = {\left( {1 + 0,01} \right)^6} \approx 1 + 6 \times 0,01 + 15 \times {\left( {0,01} \right)^2} = 1,0615\)
b) Dùng máy tính ta nhận được \(1,{01^6} \approx 1,061520151\)
-- Mod Toán 11 HỌC247
-


Tìm TXĐ của hàm số y=1/(sinx+1)
bởi Hoàng Vy
 29/11/2019
Mình thấy bài này trong ktra nhưng không biết giải mn giúp mình với
29/11/2019
Mình thấy bài này trong ktra nhưng không biết giải mn giúp mình với Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tìm hệ số x mũ 7 trong khai triển f(x)=x(2+ 3x) mũ 9
bởi Hoàng Huy
 28/11/2019
Tìm hệ số x mũ 7 trong khai triển:f(x)=x(2 3x) mũ 9Theo dõi (0) 0 Trả lời
28/11/2019
Tìm hệ số x mũ 7 trong khai triển:f(x)=x(2 3x) mũ 9Theo dõi (0) 0 Trả lời -

 tập a có 11 phần tử hỏi có bn tập con of tập hợp cóa 5 phần tửTheo dõi (0) 1 Trả lời
tập a có 11 phần tử hỏi có bn tập con of tập hợp cóa 5 phần tửTheo dõi (0) 1 Trả lời -


Hệ số s của hạng số chứa x^3 trong khai triển (1+x)^6
bởi Hồng Ngọc
 25/11/2019
hệ số s của hạng số chứa x^3 trong khai triển (1 x)^6Theo dõi (0) 2 Trả lời
25/11/2019
hệ số s của hạng số chứa x^3 trong khai triển (1 x)^6Theo dõi (0) 2 Trả lời -


Tìm hệ số của x^26 trong khai triển (1/x^4+x^7)^n
bởi Tuấn Vĩnh
 24/11/2019
Giải giúp em với ạ
24/11/2019
Giải giúp em với ạ Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Hệ số của x^5 trong khai triển (1+ x)^12?
bởi Nguyễn Thị Hương
 24/11/2019
Hệ số của x^5 trong khai triển (1 x)^12Theo dõi (0) 2 Trả lời
24/11/2019
Hệ số của x^5 trong khai triển (1 x)^12Theo dõi (0) 2 Trả lời -


Tìm số hạng thứ 200 trong khai triển (3x-1/x^2)^2019
bởi Bảo Trần
 24/11/2019
Do lúc nãy mình ghi đề sai mong mọi người giải hộ giúp mình với ạ
24/11/2019
Do lúc nãy mình ghi đề sai mong mọi người giải hộ giúp mình với ạ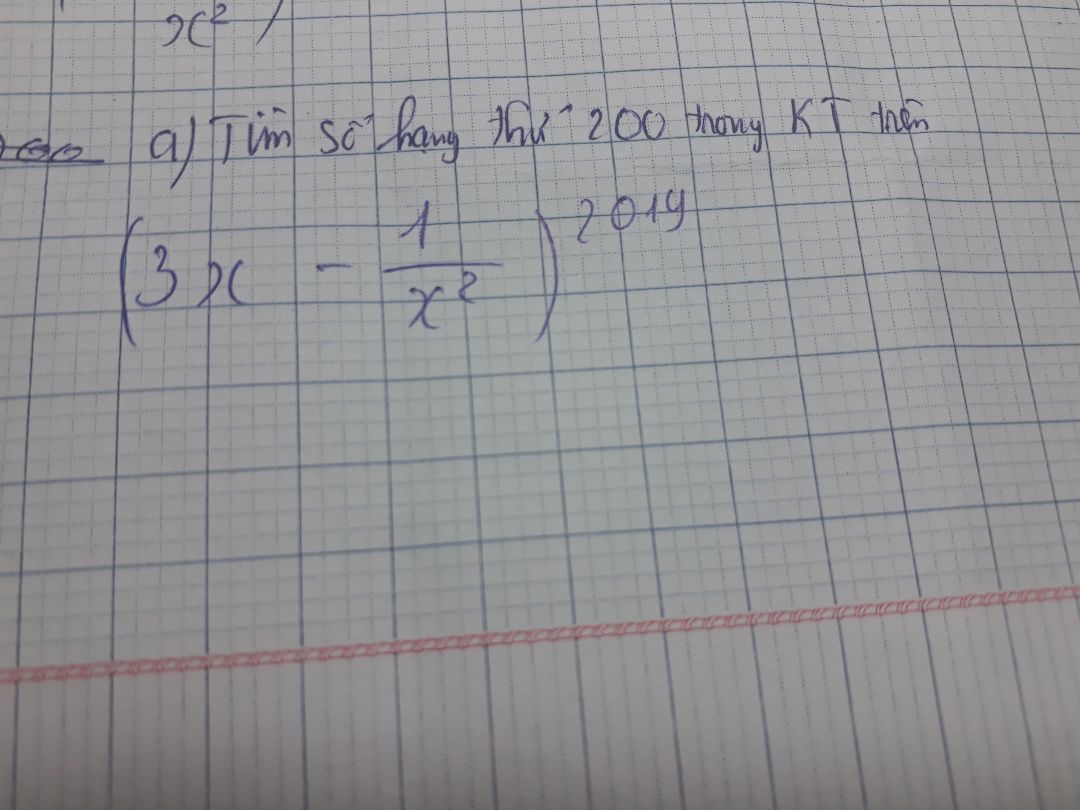 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm hệ số của x⁴y⁹ trong khai triển (x-y)¹³
bởi Kim Kim
 23/11/2019
a) Tìm hệ số của x⁴y⁹ trong khai triển (x-y)¹³b) tìm hệ số x²⁵y⁸ trong khai triển (2x³ xy²)¹¹Theo dõi (0) 1 Trả lời
23/11/2019
a) Tìm hệ số của x⁴y⁹ trong khai triển (x-y)¹³b) tìm hệ số x²⁵y⁸ trong khai triển (2x³ xy²)¹¹Theo dõi (0) 1 Trả lời -


Số (5! - p4) bằng bao nhiêu?
bởi đơn huyền cô
 23/11/2019
giải hộ mí
23/11/2019
giải hộ mí Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời
Bài tập SGK khác
Bài tập 6 trang 58 SGK Đại số & Giải tích 11
Bài tập 2.32 trang 79 SBT Toán 11
Bài tập 2.34 trang 79 SBT Toán 11
Bài tập 2.35 trang 79 SBT Toán 11
Bài tập 2.36 trang 79 SBT Toán 11
Bài tập 2.37 trang 79 SBT Toán 11
Bài tập 2.38 trang 79 SBT Toán 11
Bài tập 2.39 trang 79 SBT Toán 11
Bài tập 17 trang 67 SGK Toán 11 NC
Bài tập 18 trang 67 SGK Toán 11 NC
Bài tập 19 trang 67 SGK Toán 11 NC
Bài tập 20 trang 67 SGK Toán 11 NC
Bài tập 21 trang 67 SGK Toán 11 NC
Bài tập 22 trang 67 SGK Toán 11 NC





