Giải bài 2.32 tr 79 SBT Toán 11
Tìm số hạng thứ năm trong khai triển \({\left( {x + \frac{2}{x}} \right)^{10}}\), mà trong khai triển đó số mũ của x giảm dần.
Hướng dẫn giải chi tiết
Theo công thức Nhị thức Niu-tơn ta có
\({\left( {x + \frac{2}{x}} \right)^{10}} = \mathop \sum \limits_{k = 0}^{10} C_{10}^k{x^{10 - k}}{\left( {\frac{2}{x}} \right)^k} = \mathop \sum \limits_{k = 0}^{10} C_{10}^k{2^k}{x^{10 - 2k}}\)
Số hạng thứ k+1 trong khai triển là \({t_{k + 1}} = C_{10}^k{2^k}{x^{10 - 2k}}\)
Khi đó \({t_5} = C_{10}^4{2^4}{x^{10 - 2.4}} = C_{10}^4{2^4}{x^2} = 3360{x^2}\)
Vậy \({t_5} = 3360{x^2}\).
-- Mod Toán 11 HỌC247
-


Tìm số hạng chứa x^13 trong khai triển thành các đa thức của (x+ x^2 +x^3)
bởi Trần Bích Huệ
 13/12/2019
Tìm số hạng chứa x^13 trong khai triển thành các đa thức của (x x^2 x^3)Theo dõi (0) 0 Trả lời
13/12/2019
Tìm số hạng chứa x^13 trong khai triển thành các đa thức của (x x^2 x^3)Theo dõi (0) 0 Trả lời -


Tính S= (nC0)^2+(nC1)^2+ .....+(nCn)^2
bởi Hồng Giang
 11/12/2019
s= (nC0)^2 (nC1)^2 ..... (nCn) ^2Theo dõi (1) 0 Trả lời
11/12/2019
s= (nC0)^2 (nC1)^2 ..... (nCn) ^2Theo dõi (1) 0 Trả lời -

 Giải bài tập
Giải bài tập Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm số hạng không chứa x trong khai triển (1/căn bậc 3 của x^2+căn bậc 4 của x^3)^17
bởi Nguyễn Nhật Minh
 08/12/2019
08/12/2019
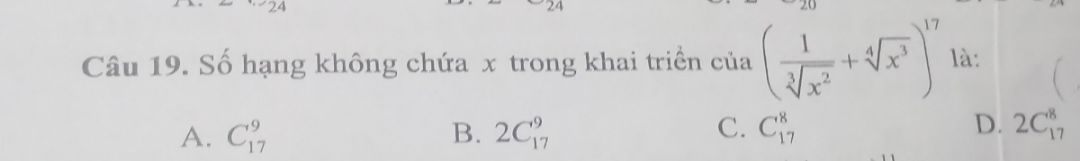 Theo dõi (1) 9 Trả lời
Theo dõi (1) 9 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Tìm hệ số x^9 trong khai triển nhị thức Newton sau:(1 2x).(3 x)^11Theo dõi (1) 2 Trả lời
Tìm hệ số x^9 trong khai triển nhị thức Newton sau:(1 2x).(3 x)^11Theo dõi (1) 2 Trả lời -


Tìm số hạng không chứa x trong khai triển (2x-1/x^2)^6
bởi Giang Trà
 03/12/2019
Giúp mình với!! Cảm ơn^-^
03/12/2019
Giúp mình với!! Cảm ơn^-^ Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -

 Giải bt tập này nhanh giúp tôi với
Giải bt tập này nhanh giúp tôi với Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -

 Cho P(x) = (x-1/4)^n. Tìm hệ số tự nhiên n, biết rằng hệ số của x^n-2 trong P(x) bằng 31Theo dõi (0) 0 Trả lời
Cho P(x) = (x-1/4)^n. Tìm hệ số tự nhiên n, biết rằng hệ số của x^n-2 trong P(x) bằng 31Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 5 trang 58 SGK Đại số & Giải tích 11
Bài tập 6 trang 58 SGK Đại số & Giải tích 11
Bài tập 2.33 trang 79 SBT Toán 11
Bài tập 2.34 trang 79 SBT Toán 11
Bài tập 2.35 trang 79 SBT Toán 11
Bài tập 2.36 trang 79 SBT Toán 11
Bài tập 2.37 trang 79 SBT Toán 11
Bài tập 2.38 trang 79 SBT Toán 11
Bài tập 2.39 trang 79 SBT Toán 11
Bài tập 17 trang 67 SGK Toán 11 NC
Bài tập 18 trang 67 SGK Toán 11 NC
Bài tập 19 trang 67 SGK Toán 11 NC
Bài tập 20 trang 67 SGK Toán 11 NC
Bài tập 21 trang 67 SGK Toán 11 NC
Bài tập 22 trang 67 SGK Toán 11 NC





