Giải bài 2.36 tr 79 SBT Toán 11
Xác định hệ số của số hạng chứa x4 trong khai triển \({\left( {{x^2} - \frac{2}{x}} \right)^n}\) nếu biết tổng các hệ số của ba số hạng đầu trong khai triển đó bằng 97.
Hướng dẫn giải chi tiết
Ta có \({\left( {{x^2} - \frac{2}{x}} \right)^n} = C_n^0{\left( {{x^2}} \right)^n} + C_n^1{\left( {{x^2}} \right)^{n - 1}}.\left( { - \frac{2}{x}} \right) + C_n^2{\left( {{x^2}} \right)^{n - 2}}.{\left( { - \frac{2}{x}} \right)^2} + ...\)
Theo giả thiết, ta có:
\(\begin{array}{*{20}{l}}
{C_n^0 - 2C_n^1 + 4C_n^2 = 97 \Leftrightarrow 1 - 2n + 2n\left( {n - 1} \right) - 97 = 0}\\
{ \Leftrightarrow {n^2} - 2n - 48 = 0}\\
{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{n = 8}\\
{n = - 6\,\,\left( {\rm{l}} \right)}
\end{array}} \right.}
\end{array}\)
Vậy n = 8 Từ đó ta có:
\({\left( {{x^2} - \frac{2}{x}} \right)^8} = \mathop \sum \limits_{k = 0}^8 C_8^k{\left( {{x^2}} \right)^{8 - k}}{\left( { - \frac{2}{x}} \right)^k} = \mathop \sum \limits_{k = 0}^8 {\left( { - 2} \right)^k}.C_8^k.{x^{16 - 3k}}\)
Như vậy, ta phải có \(16 - 3k = 4 \Leftrightarrow k = 4\) Do đó hệ số của số hạng chứa x4 là \({\left( { - 2} \right)^4}.C_8^4 = 1120\).
-- Mod Toán 11 HỌC247
-


Tìm hệ số của x^7 trong f(x) =(1-2x)^10
bởi Hồ Thien
 27/10/2019
tìm hệ số của x^7 trong fx =(1-2x)^10Theo dõi (0) 4 Trả lời
27/10/2019
tìm hệ số của x^7 trong fx =(1-2x)^10Theo dõi (0) 4 Trả lời -


Khai triển (x +1/x)^4
bởi Thucky Duong
 23/10/2019
Khai triển (x 1/x)^4Theo dõi (1) 2 Trả lời
23/10/2019
Khai triển (x 1/x)^4Theo dõi (1) 2 Trả lời -


Tìm hệ số x^7 trong khai triển (3x^2 - 2/x)^n
bởi TrịNh MiNh Hiếu
 08/10/2019
Tìm hệ số x^7 trong khai triển (3x^2 - 2/x)^n biết hệ số của số hạng thứ ba trong khai triển bằng 1080Theo dõi (0) 2 Trả lời
08/10/2019
Tìm hệ số x^7 trong khai triển (3x^2 - 2/x)^n biết hệ số của số hạng thứ ba trong khai triển bằng 1080Theo dõi (0) 2 Trả lời -


Tìm hệ số của x^8 trong khai triển (1+2x^2-3x^3)^9
bởi Ly Phương
 27/09/2019
Cho em hỏi ví dụ 6 vs ạ? Em cảm ơn ạ
27/09/2019
Cho em hỏi ví dụ 6 vs ạ? Em cảm ơn ạ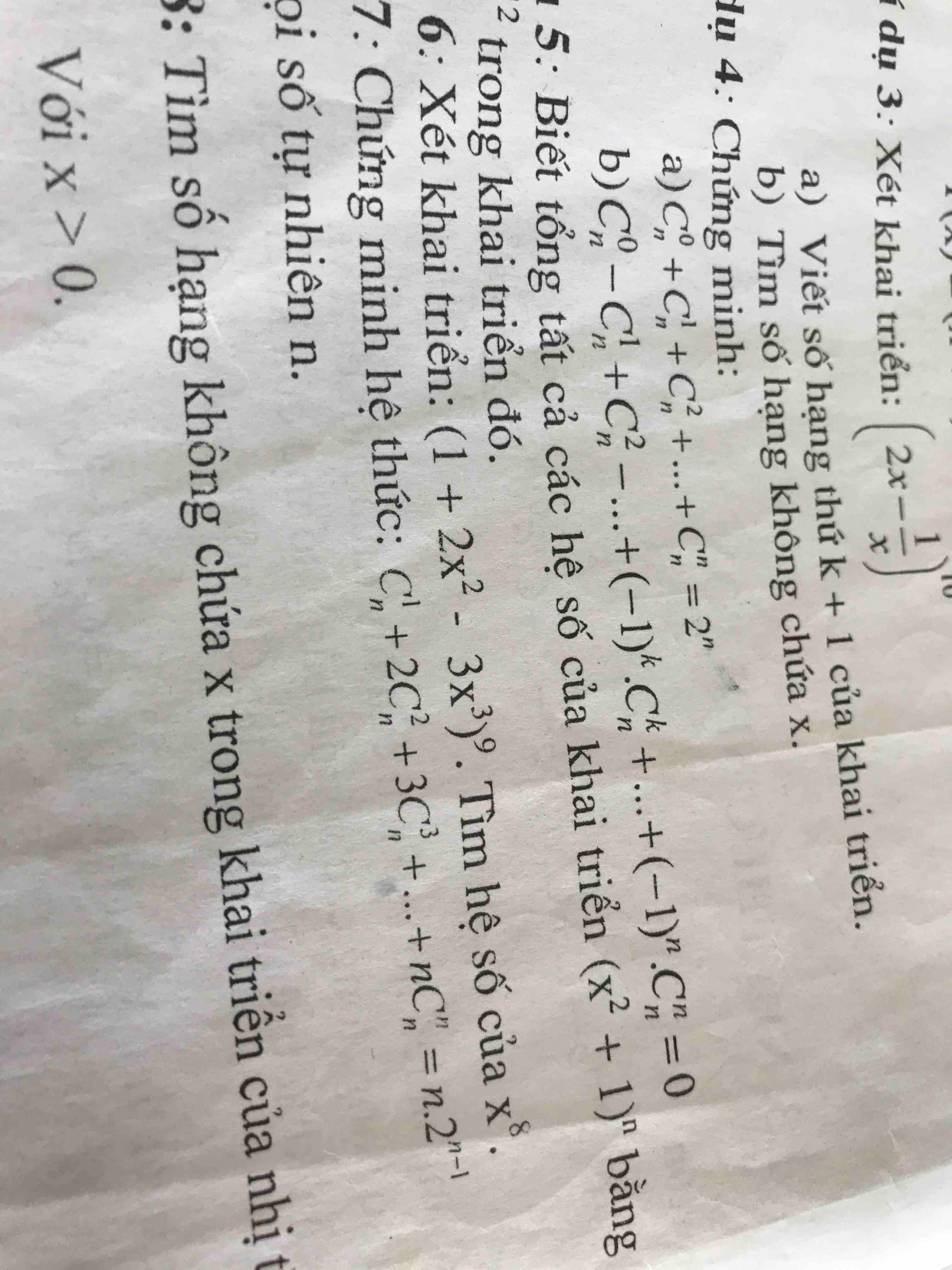 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Trong khai triển nhị thức (2x^3 2/x^2)^10 hãy tìm số hạng không phụ thuộc xTheo dõi (0) 0 Trả lời
Trong khai triển nhị thức (2x^3 2/x^2)^10 hãy tìm số hạng không phụ thuộc xTheo dõi (0) 0 Trả lời -


Tìm hệ số của x^4 trong khai triển (2x+1/x)^8
bởi Vũ Đình Nam
 25/06/2019
Ai bày e cách làm vs ạ
25/06/2019
Ai bày e cách làm vs ạ Theo dõi (1) 7 Trả lời
Theo dõi (1) 7 Trả lời -


Tính tổng S=a0-a2+a4-a6+...-a4034+a4036
bởi Nguyễn Đạt
 04/01/2019
04/01/2019
cho (x2+x+1)2018 , khai triển ra đc a0+a1x+...+a4036x4036.Tìm tổng S=a0-a2+a4-a6+...-a4034+a4036
Theo dõi (1) 0 Trả lời -


trong khai triển P(x)= (2/x+X2 )20
a. tìm số hạng không chứa x
b. tìm số hạng chứa x10
giải giúp em với ạ. em tính ra câu a số nhỏ câu b số lớn nên hơi nghi nghi :)) help me
Theo dõi (0) 3 Trả lời -


Tính A=(3+1/3)^2+(3^2+1/3^2)^2+....+(3^n+1/3^n)^2
bởi Nguyễn Tấn Hiệp
 18/12/2018
18/12/2018
Tính các tổng sau:
A= (3+1/3)2+(32+1/32)2+....+(3n+1/3n)2
Theo dõi (1) 4 Trả lời
Bài tập SGK khác
Bài tập 2.34 trang 79 SBT Toán 11
Bài tập 2.35 trang 79 SBT Toán 11
Bài tập 2.37 trang 79 SBT Toán 11
Bài tập 2.38 trang 79 SBT Toán 11
Bài tập 2.39 trang 79 SBT Toán 11
Bài tập 17 trang 67 SGK Toán 11 NC
Bài tập 18 trang 67 SGK Toán 11 NC
Bài tập 19 trang 67 SGK Toán 11 NC
Bài tập 20 trang 67 SGK Toán 11 NC
Bài tập 21 trang 67 SGK Toán 11 NC
Bài tập 22 trang 67 SGK Toán 11 NC





