Giải bài 2 tr 119 sách GK Toán Hình lớp 11
Cho tứ diện S.ABC có SA vuông góc với mặt phẳng (ABC). Gọi H, K lần lượt là trực tâm của tam giác ABC và SBC.
a) Chứng minh ba đường thẳng AH, SK, BC đồng quy.
b) Chứng minh rằng SC vuông góc với mặt phẳng (BHK) và HK vuông góc với mặt phẳng (SBC).
c) Xác định đường vuông góc chung của BC và SA
Hướng dẫn giải chi tiết
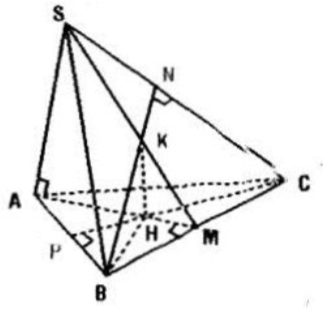
Câu a:
Gọi M là chân đường cao hạ từ S xuống BC vì \(SA\perp (ABC)\Rightarrow AM\) là hình chiếu vuông góc của SM trên mặt phẳng (ABC).
Vì \(SM\perp BC\Rightarrow AM\perp BC\) (theo định lí ba đường vuông góc)
Vì H, K là trực tâm của \(\Delta ABC, \Delta SBC\) nên AH, SK và BC đồng quy tại M (đpcm).
Câu b:
Vì H là trực tâm của tam giác \(ABC\Rightarrow BH\perp AC \ (1)\)
Vì \(SA\perp (ABC);BH\subset (SAC)\Rightarrow BH\perp SA \ (2)\)
Từ (1) và (2) suy ra \(BH \perp (SAC)\Rightarrow BH\perp SC \ (3)\)
Vì K là trực tâm của \(\Delta SBC\Rightarrow BK\perp SC \ (4)\)
Từ (3) và (4) suy ra \(SC\perp (BHK)\) (đpcm)
Theo chứng minh trên \(SC\perp (BHK)\Rightarrow HK\perp SC \ (5)\)
Mặt khác do \(AM\perp BC\) và \(SM\perp BC\Rightarrow BC\perp (ASM)\Rightarrow BC\perp HK \ (6)\)
Từ (5) và (6) suy ra \(HK\perp (SBC)\) (đpcm)
Câu c:
Dễ thấy AM là đường vuông góc chung của BC và SA.
-- Mod Toán 11 HỌC247
Để luyện tập thêm dạng bài tương tự như Bài tập 2 trang 119 trong SGK các em làm thêm câu hỏi trắc nghiệm sau để cũng cố kỹ năng làm dạng bài.
-
Câu 1:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SD = \frac{{a\sqrt {17} }}{2}\), hình chiếu vuông góc H của S lên mặt (ABCD) là trung điểm của đoạn AB. Tính chiều cao h của khối chóp H.SBD theo a.
- A. \(h = \frac{{\sqrt 3 a}}{2}\)
- B. \(h = \frac{{a\sqrt 3 }}{7}\)
- C. \(h = \frac{{a\sqrt {21} }}{2}\)
- D. \(h = \frac{{3a}}{5}\)
-
Bài 3.33 trang 162 sách bài tập Hình học 11
bởi Thiên Mai
24/10/2018
Bài 3.33 (Sách bài tập - trang 162)Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng khoảng cách từ các điểm A', B, D; C, B', D' tới đường chéo AC' bằng nhau. Tính khoảng cách đó ?
Theo dõi (0) 1 Trả lời -
Cho ltrụ đứng ABCA'B'C' có AC=a BC=2a, góc ACB=120°. Góc giữa A'C và (ABB'A') bằng 30°. M là trung điểm cua BB'. Tính khoang cach từ A' đên ACM
Theo dõi (0) 1 Trả lời -
Bài 5 trang 119 SGK Hình học 11
bởi Van Tho
24/10/2018
Bài 5 (SGK trang 119)Cho hình lập phương ABCD.A'B'C'D' cạnh a
a) Chứng minh rằng B'D vuông góc với mặt phẳng (BA'C')
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD')
c) Tính khoảng cách giữa hai đường thẳng BC' và CD'
Theo dõi (0) 1 Trả lời -
Hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD=2AB=2a. SA=2a và SA vuông góc đáy.M,N lần lượt là trung điểm SB&SD. Tìm khoảng cách từ S đến mp(AMN).
Theo dõi (0) 1 Trả lời
Được đề xuất cho bạn
