Bài tập 34 trang 118 SGK Hình học 11 NC

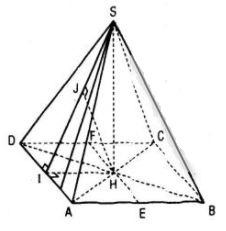
a) Vì SA = SB = SC = SD = \(a\sqrt 2 \) nên hình chiếu của điểm S trên mặt phẳng (ABCD) là điểm H mà HA = HB = HC = HD.

Do ABCD là hình chữ nhật nên H chính là giao điểm của AC và BD.

Khoảng cách từ S đến mp(ABCD) bằng SH. Ta có:

\(\begin{array}{*{20}{l}}
\begin{array}{l}
S{H^2} = S{A^2} - \frac{{A{C^2}}}{4}\\
 = 2{a^2} - \frac{{A{B^2} + B{C^2}}}{4}
\end{array}\\
{ = 2{a^2} - \frac{{4{a^2} + {a^2}}}{4} = \frac{{3{a^2}}}{4}}\\
{ \Rightarrow SH = \frac{{a\sqrt 3 }}{2}}
\end{array}\)

b) Vì EF // AD nên EF // mp(SAD), mặt khác SK nằm trong mp(SAD) nên khoảng cách giữa EF và SK chính là khoảng cách giữa EF và mp(SAD), đó cũng chính là khoảng cách từ H đến mp(SAD).

Vậy khoảng cách giữa EF và SK không phụ thuộc vào vị trí của điểm K trên đường thẳng AD.

Tính d(EF ; SK) :

Gọi I là trung điểm của AD, kẻ đường cao HJ của tam giác vuông SHI thì HJ ⊥ mp(SAD), do đó d(H; (SAD)) = HJ.

Ta có: HJ.SI = SH.HI

\(\begin{array}{*{20}{l}}
\begin{array}{l}
S{I^2} = S{A^2} - A{I^2}\\
 = 2{a^2} - \frac{{{a^2}}}{4} = \frac{{7{a^2}}}{4}
\end{array}\\
\begin{array}{l}
 \Rightarrow HJ = \frac{{SH.HI}}{{SI}}\\
 = \frac{{\frac{{a\sqrt 3 }}{2}.a}}{{\frac{{a\sqrt 7 }}{2}}} = \frac{{a\sqrt {21} }}{7}
\end{array}
\end{array}\)

Vậy khoảng cách giữa EF và SK không phụ thuộc vào vị trí của điểm K trên đường thẳng AD và bằng \(\frac{{a\sqrt {21} }}{7}\).

-- Mod Toán 11 HỌC247