Giải bài 3.38 tr 160 SBT Hình học 11
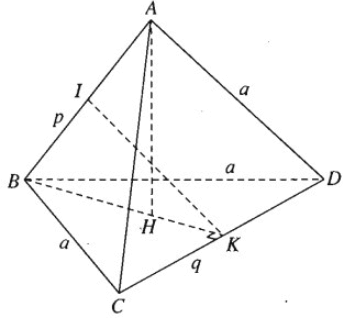
Tính khoảng cách giữa hai cạnh AB và CD của hình tứ diện ABCD biết rằng AC = BC = AD = BD = a và AB = p, CD = q.
Hướng dẫn giải chi tiết
Gọi I và K lần lượt là trung điểm của AB và CD, ta có IK là đoạn vuông góc chung của AB và CD và độ dài đoạn IK là khoảng cách cần tìm.
\(I{K^2} = B{K^2} - B{I^2} = B{K^2} - \frac{{{p^2}}}{4}\)
Mà \(B{K^2} = B{C^2} - C{K^2} = {a^2} - \frac{{{q^2}}}{4}\) nên \(B{K^2} = B{C^2} - C{K^2} = {a^2} - \frac{{{q^2}}}{4}\)
Do đó \(B{K^2} = B{C^2} - C{K^2} = {a^2} - \frac{{{q^2}}}{4}\) với điều kiện \(4{a^2} - \left( {{p^2} + {q^2}} \right) > 0\).
-- Mod Toán 11 HỌC247
-
Tính khoảng cách cách từ B đến mặt phẳng SAC biết đáy tam giác vuông tại A
bởi Golden Meadow
14/08/2018
Cho hình chóp SABC đáy tam giác vuông tại A, AB= a, AC = a√3. Tam giác SBC đều và nằm trong mặt phẳng vuông tới đáy. Tính khoảng cách cách từ B đến mặt phẳng SAC
Theo dõi (0) 0 Trả lời -
Tính khoảng cách từ B đến mp (SBC) biết SC hợp (ABCD) một góc am pha với tan ampha= 4/5
bởi Hưng Aristino
10/08/2018
cho hình chóp SABCD có đáy abcd là hình chữ nhật, SA vuông góc vs đáy, SC hợp (ABCD) một góc am pha với tan ampha= 4/5, AB=3a, BC=4a . khoảng cách từ B đến (SBC) là
Theo dõi (0) 0 Trả lời -
Tính góc giữa hai đường thẳng BF và AC biết SA vuông góc với mặt phẳng (ABCD),SA=2a
bởi Phương Duy
22/07/2018
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD),SA=2a . Gọi F là trung điểm SC, tính góc j giữa hai đường thẳng BF và AC.
Theo dõi (0) 1 Trả lời -
Tính khoảng cách từ C đến mặt phẳng (BMB') biết đáy ABC là tam giác vuông tại B, AB=a
bởi Thu Huyền
30/06/2018
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AB=a, góc ACB = 30 độ. M là trung điểm cạnh AC. Góc giữa cạnh bên và mặt đáy của lăng trụ bằng 60 độ. Hình chiếu vuông góc của đỉnh A' lên mặt phẳng (ABC) là trung điểm H của BM. Tính theo a khoảng cách từ C đến mặt phẳng (BMB').
Theo dõi (0) 0 Trả lời -
Tính khoảng cách từ trọng tâm G của tam giác SAD đến mặt phẳng (SBM) biết AD=2AB=2BC
bởi Thu Huyền
30/06/2018
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B,AD=2AB=2BC, CD=2a căn 2. Hình chiếu vuông góc của S trên mặt đáy là trung điểm M của cạnh CD. Tính khoảng cách từ trọng tâm G của tam giác SAD đến mặt phẳng (SBM).
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 3.36 trang 160 SBT Hình học 11
Bài tập 3.37 trang 160 SBT Hình học 11
Bài tập 3.39 trang 160 SBT Hình học 11
Bài tập 3.40 trang 160 SBT Hình học 11
Bài tập 29 trang 117 SGK Hình học 11 NC
Bài tập 30 trang 117 SGK Hình học 11 NC
Bài tập 31 trang 117 SGK Hình học 11 NC
Bài tập 32 trang 117 SGK Hình học 11 NC
Bài tập 33 trang 118 SGK Hình học 11 NC
