Bài tập 30 trang 117 SGK Hình học 11 NC
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt đáy bằng 30˚. Hình chiếu H của điểm A trên mặt phẳng (A’B’C’) thuộc đường thẳng B’C’.
a. Tính khoảng cách giữa hai mặt phẳng đáy
b. Chứng minh rằng hai đường thẳng AA’ và B’C’ vuông góc, tính khoảng cách giữa chúng.
Hướng dẫn giải chi tiết
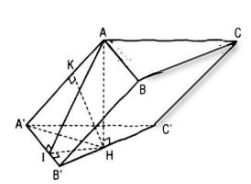
Ta có: AH ⊥ (A’B’C’) nên \(\widehat {AA'H}\) là góc giữa AA’ và mp(A’B’C’) do đó \(\widehat {AA'H}\) = 300
a) Khoảng cách giữa hai mp đáy chính là AH, ta có:
\(AH = AA\prime sin{30^0} = \frac{a}{2}\)
b) Tam giác AHA’ vuông tại H nên \(A\prime H = AA\prime cos{30^0} = \frac{{a\sqrt 3 }}{2}\).
Vì A’B’C’ là tam giác đều cạnh a, H thuộc đường thẳng B’C’ mà \(A\prime H = \frac{{a\sqrt 3 }}{2}\) nên A’H ⊥ B’C’ và H là trung điểm B’C’.
Mặt khác, AH ⊥ B’C’ nên AA’ ⊥ B’C’. Kẻ đường cao HK của tam giác AA’H thì HK chính là khoảng cách giữa AA’ và B’C’.
Do AA’.HK = AH.A’H nên
\(HK = \frac{{\frac{a}{2}.\frac{{a\sqrt 3 }}{2}}}{a} = \frac{{a\sqrt 3 }}{4}\)
-- Mod Toán 11 HỌC247
-


Tính khoảng cách giữa hai đường thẳng chéo nhau
bởi Tran Sa
 13/08/2017
13/08/2017
Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Biết AC=2a, BD=3a. Tính khoảng cách giữa AD và SC.
Theo dõi (1) 2 Trả lời -


Tính d(MN;(SCD)) biết M,N là trung điểm của SA,SB
bởi Tam Thiên
 11/08/2017
11/08/2017
Hchóp SABCD SA vuông góc (ABCD) . ABCD là hình chữ nhật .AB=a,AD=2a, SA=3a .M,N là trung điểm của SA,SB
Tính d(MN;(SCD))
Theo dõi (0) 2 Trả lời -


H.chóp SABCD . SA,SB,SC cùng tạo với (ABC) góc 60* .ABCD là h.thang vuông tại A và B, AB=BC=a , AD=2a
a,Tính :d(AD;(SCB))
b,M là trung điểm AD .Tính d(BM;(SCD))
Theo dõi (0) 0 Trả lời -


H.hộp chữ nhật ABCDA'B'C'D' .AB=a AD=2a AA'=3a .Tính :
a,d(AA';(BB'C))
b,d(AC;(BA'C'))
Theo dõi (0) 3 Trả lời -


Tính khoảng cách giữa CB và SD biết hình chóp S.SBCD có đáy ABCD là hình vuông cạnh a
bởi Tran Sa
 10/08/2017
10/08/2017
Cho hình chóp S.SBCD có đáy ABCD là hình vuông cạnh a, SA⊥(ABCD), góc giữa SB và mp(ABCD) là 600 . Khoảng cách từ CB đến SD là
Theo dõi (2) 2 Trả lời





