Giải bài 6 tr 119 sách GK Toán Hình lớp 11
Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD của tứ diện ABCD là đường vuông góc chung của AB và CD thì AC = BD và AD = BC.
Hướng dẫn giải chi tiết
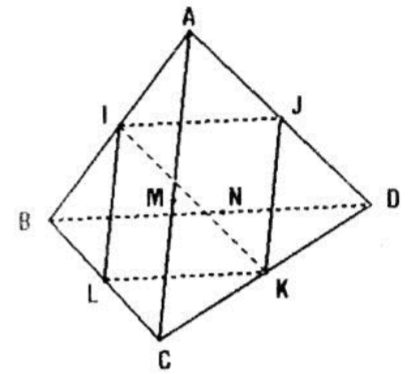
Gọi I, J, K, L, M, N lần lượt là trung điểm của AB, AD, CD, BC, AC, BD
Ta có: \(\left.\begin{matrix} IK\perp CD\\ IJ // CD \end{matrix}\right\} \Rightarrow IK \perp JM \ (1)\)
Và \(\left.\begin{matrix} IK\perp AB\\ JN // AB \end{matrix}\right\} \Rightarrow IK \perp JN \ (2)\)
Từ (1) và (2) suy ra \(IK \perp (JMLN)\)
\(\Rightarrow IK\perp JL\)
Mặt khác IJKL là hình bình hành
⇒ IJKL là hình thoi ⇒ IJ = JK
Mà BD = 2IJ; AC = 2JK ⇒ BD = AC.
Chứng minh tương tự ta cũng được: AD = BC.
Vậy AD = BC và BD = AC (đpcm).
-- Mod Toán 11 HỌC247
-
Câu 26
Theo dõi (0) 0 Trả lời -
Tính khoảng cách từ G đến mặt phẳng (HMN)?
bởi Híp
21/06/2020
Cho hình chóp SABCD có đáy là hình thoi cạnh a, góc ABC bằng 60 độ. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy, gọi H, M, N lần lượt là trung điểm của các cạnh AB, SA, SD và G là trọng tâm tam giác SBC. Khoảng cách từ G đến mặt phẳng (HMN) bằng
Theo dõi (0) 0 Trả lời -
Tính khoảng cách từ M đến mp(SBC)?
bởi Nguyễn Công Tuấn.A
20/06/2020
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a; cạnh bên SA vuông góc với mặt đáy, SA=a√3SA=a3; gọi M là trung điểm AC. Tính khoảng cách từ M đến mp(SBC).Theo dõi (0) 1 Trả lời -
Tính khoảng cách hai đường thẳng AB và SC?
bởi Nguyễn Phước Tiến
16/06/2020
Giúp em với
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy (ABCD),SA = a√2 .Tính khoảng cách hai đường thẳng AB và SC.
Theo dõi (0) 1 Trả lời -
Giúp em giải với em cần gấp
Cho hình chóp S.ABCD có ABCD là hình vuông tâm O cạnh a . SA vuông góc với (ABCD) và SA=a√2. Xác định và tính góc giữa hai mp ( SBC) và mp ( ABCD)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 4 trang 119 SGK Hình học 11
Bài tập 5 trang 119 SGK Hình học 11
Bài tập 7 trang 119 SGK Hình học 11
Bài tập 8 trang 119 SGK Hình học 11
Bài tập 3.33 trang 160 SBT Hình học 11
Bài tập 3.34 trang 160 SBT Hình học 11
Bài tập 3.35 trang 160 SBT Hình học 11
Bài tập 3.36 trang 160 SBT Hình học 11
Bài tập 3.37 trang 160 SBT Hình học 11
Bài tập 3.38 trang 160 SBT Hình học 11
Bài tập 3.39 trang 160 SBT Hình học 11
Bài tập 3.40 trang 160 SBT Hình học 11
Bài tập 29 trang 117 SGK Hình học 11 NC
Bài tập 30 trang 117 SGK Hình học 11 NC
Bài tập 31 trang 117 SGK Hình học 11 NC
Bài tập 32 trang 117 SGK Hình học 11 NC
Bài tập 33 trang 118 SGK Hình học 11 NC
