Giải bài 3.33 tr 160 SBT Hình học 11
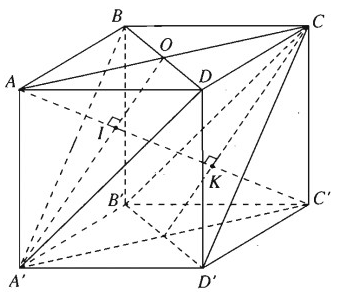
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng khoảng cách từ các điểm A', B, D; C, B', D tới đường chéo AC' bằng nhau. Tính khoảng cách đó.
Hướng dẫn giải chi tiết
Điểm A cách đều ba đỉnh của tam giác đều A'BD vì ta có AB = AD = AA′ = a, điểm C' cũng cách đều ba đỉnh của tam giác đều đó vì ta có C′B = C′D = C′A′ = \(a\sqrt 2 \).
Vậy AC' là trục của đường tròn ngoại tiếp tam giác A'BD, tức là đường thẳng AC' vuông góc với mặt phẳng (A'BD) tại trọng tâm I của tam giác A'BD. Ta cần tìm khoảng cách A'I.
Ta có \(A'I = BI = DI = \frac{{2A'O}}{3}\) với O là tâm của hình vuông ABCD.
Ta lại có \(AO' = \frac{{BD\sqrt 3 }}{2} = \frac{{a\sqrt 2 .\sqrt 3 }}{2} = \frac{{a\sqrt 6 }}{2}\)
Vậy \(A'I = \frac{2}{3}A'O = \frac{2}{3}.\frac{{a\sqrt 6 }}{2} = \frac{{a\sqrt 6 }}{3}\)
Tương tự điểm C' cách đều ba đỉnh của tam giác đều CB'D', tính được khoảng cách từ C, B', D' tới đường chéo AC'.
-- Mod Toán 11 HỌC247
-


Tính khoảng cách từ H đến mp(SCD) biết hình chóp S.ABCD là hình thang vuông tại A và B
bởi Anh Nguyễn Thế
 13/05/2020
13/05/2020
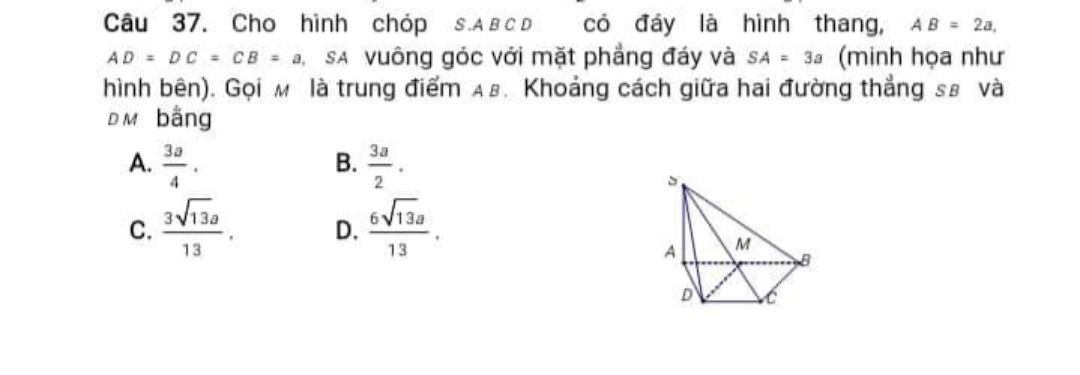
cho hình chóp S.ABCD là hình thang vuông tại A và B. biết AD=2a, AB=BC=a, SA vuông góc mp(ABCD), SA =a√3, điểm H thuộc SB sao cho 3SH=SB. tính khoảng cách từ H đến mp(SCD)
Theo dõi (0) 1 Trả lời -


Tính khoảng cách giữa hai đường thẳng NP và SB thao a?
bởi Gia Trang
 05/05/2020
Mn giúp mình với cảm ơn nhiều
05/05/2020
Mn giúp mình với cảm ơn nhiều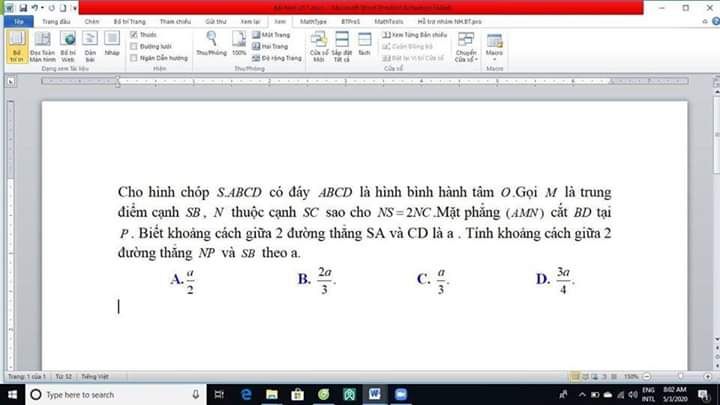 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Khoảng cách giữa hai đường thẳng SB và DM là?
bởi Linh Ly
 13/04/2020
13/04/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng căn 3, góc BAD=120 độ, SA vuông góc với (ABCD) biết góc giữa (SBC) và (ABCD) là 60 độ. Tính khoảng cách BD và SC.
bởi Ngọc Mai
 03/04/2020
cho hình chóp sabcd có đáy abcd là hình thoi cạnh bằng căn 3 bad=120 sa vuông góc với abcd biết goc giữa sbc và abcd là 60 tính khoảng cách bd sc
03/04/2020
cho hình chóp sabcd có đáy abcd là hình thoi cạnh bằng căn 3 bad=120 sa vuông góc với abcd biết goc giữa sbc và abcd là 60 tính khoảng cách bd sc Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 7 trang 119 SGK Hình học 11
Bài tập 8 trang 119 SGK Hình học 11
Bài tập 3.34 trang 160 SBT Hình học 11
Bài tập 3.35 trang 160 SBT Hình học 11
Bài tập 3.36 trang 160 SBT Hình học 11
Bài tập 3.37 trang 160 SBT Hình học 11
Bài tập 3.38 trang 160 SBT Hình học 11
Bài tập 3.39 trang 160 SBT Hình học 11
Bài tập 3.40 trang 160 SBT Hình học 11
Bài tập 29 trang 117 SGK Hình học 11 NC
Bài tập 30 trang 117 SGK Hình học 11 NC
Bài tập 31 trang 117 SGK Hình học 11 NC
Bài tập 32 trang 117 SGK Hình học 11 NC
Bài tập 33 trang 118 SGK Hình học 11 NC