Giải bài 3.35 tr 160 SBT Hình học 11
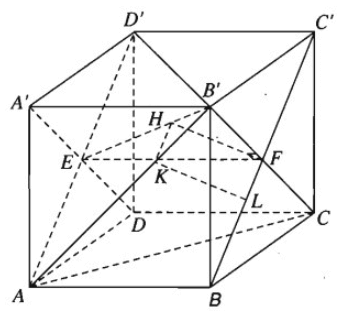
Cho hình lập phương ABCD.A'B'C'D'.
a) Chứng minh đường thẳng BC' vuông góc với mặt phẳng (A'B'CD)
b) Xác định và tính độ dài đoạn vuông góc chung của AB' và BC'.
Hướng dẫn giải chi tiết
a) Ta có B'C ⊥ BC' vì đây là hai đường chéo của hình vuông BB'C'C.
Mặt khác: A'B' ⊥ (BB'C'C) ⇒ A'B' ⊥ BC'
Từ đó ta suy ra BC' ⊥ (A'B'CD) vì mặt phẳng (A'B'CD) chứa đường thẳng A'B' và B'C cùng vuông góc với BC'.
b) Mặt phẳng (AB'D') chứa đường thẳng AB' và song song với BC', ta tìm hình chiếu của BC' trên mặt phẳng (AB'D').
Gọi E, F lần lượt là tâm các hình vuông ADD'A', BCC'B'.
Kẻ FH ⊥ EB' với H ∈ EB', khi đó FH nằm trên mặt phẳng (A'B'CD) nên theo câu a) thì FH ⊥ (AB'D')
Do đó hình chiếu BC' trên mặt phẳng (AB'D) là đường thẳng đi qua H và song song với BC'.
Giả sử đường thẳng đó cắt AB' tại K thì từ K vẽ đường thẳng song song với FH cắt BC' tại L. Khi đó KL là đoạn vuông góc chung cần dựng.
Tam giác B'EF vuông tại F nên từ công thức \(\frac{1}{{F{H^2}}} = \frac{1}{{F{E^2}}} + \frac{1}{{F{B^2}}}\) tính được \(KL = FH = \frac{{a\sqrt 3 }}{3}\)
-- Mod Toán 11 HỌC247
-


Bài 3.38 trang 162 sách bài tập Hình học 11
bởi Bánh Mì
 24/10/2018
Bài 3.38 (Sách bài tập - trang 162)
24/10/2018
Bài 3.38 (Sách bài tập - trang 162)Tính khoảng cách giữa hai cạnh AB và CD của tứ diện ABCD biết rằng AC = BC = AD = BD = a và AB = p, CD = q ?
Theo dõi (0) 1 Trả lời -


Bài 3.33 trang 162 sách bài tập Hình học 11
bởi Thiên Mai
 24/10/2018
Bài 3.33 (Sách bài tập - trang 162)
24/10/2018
Bài 3.33 (Sách bài tập - trang 162)Cho hình lập phương ABCD.A'B'C'D' cạnh a. Chứng minh rằng khoảng cách từ các điểm A', B, D; C, B', D' tới đường chéo AC' bằng nhau. Tính khoảng cách đó ?
Theo dõi (0) 1 Trả lời -


Cho ltrụ đứng ABCA'B'C' có AC=a BC=2a, góc ACB=120°. Góc giữa A'C và (ABB'A') bằng 30°. M là trung điểm cua BB'. Tính khoang cach từ A' đên ACM
Theo dõi (0) 1 Trả lời -


Bài 5 trang 119 SGK Hình học 11
bởi Van Tho
 24/10/2018
Bài 5 (SGK trang 119)
24/10/2018
Bài 5 (SGK trang 119)Cho hình lập phương ABCD.A'B'C'D' cạnh a
a) Chứng minh rằng B'D vuông góc với mặt phẳng (BA'C')
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD')
c) Tính khoảng cách giữa hai đường thẳng BC' và CD'
Theo dõi (0) 1 Trả lời -


Hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD=2AB=2a. SA=2a và SA vuông góc đáy.M,N lần lượt là trung điểm SB&SD. Tìm khoảng cách từ S đến mp(AMN).
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3.33 trang 160 SBT Hình học 11
Bài tập 3.34 trang 160 SBT Hình học 11
Bài tập 3.36 trang 160 SBT Hình học 11
Bài tập 3.37 trang 160 SBT Hình học 11
Bài tập 3.38 trang 160 SBT Hình học 11
Bài tập 3.39 trang 160 SBT Hình học 11
Bài tập 3.40 trang 160 SBT Hình học 11
Bài tập 29 trang 117 SGK Hình học 11 NC
Bài tập 30 trang 117 SGK Hình học 11 NC
Bài tập 31 trang 117 SGK Hình học 11 NC
Bài tập 32 trang 117 SGK Hình học 11 NC
Bài tập 33 trang 118 SGK Hình học 11 NC