Giải bài 5 tr 119 sách GK Toán Hình lớp 11
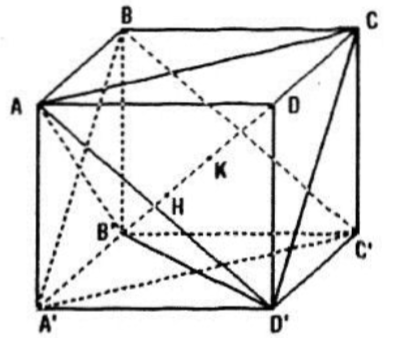
Cho hình lập phương ABCD.A'B'C'D' cạnh a.
a) Chứng minh rằng B'D vuông góc với mặt phẳng (BA'C').
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD').
c) Tính khoảng cách giữa hai đường thẳng BB' vad AC'.
Hướng dẫn giải chi tiết
Câu a:
Vì ABB'A' là hình vuông nên \(A'B\perp AB'\) lại thấy \(AD\perp (ABB'A')\Rightarrow AD\perp A'B\) suy ra \(A'B\perp (ADB')\Rightarrow A'B\perp DB' \ (1)\)
Do A'B'C'D' là hình vuông \(\Rightarrow A'C'\perp B'D', DD'\perp (A'B'C'D')\Rightarrow DD'\perp A'C'\)
Suy ra \(A'C'\perp (DB'D')\Rightarrow A'C'\perp B'D \ (2)\)
Từ (1) và (2) suy ra \(B'D\perp (A'C'B)\)
Câu b:
Gọi H và K lần lượt là giao điểm của B'D với mặt phẳng (BA'C') và mặt phẳng (ACD')
Ta đã chứng minh được \(B'D\perp (BA'C')\) và \((BA'C') //(ACD')\Rightarrow DK\perp (ACD')\) và \(B'H\perp (BA'C')\)
Dễ thấy \(AC=AD'=CD'=a\sqrt{2}\) (giả sử cạnh của hình lập phường là a) và \(DK\perp (ACD')\Rightarrow \frac{1}{DK^2}= \frac{1}{DA^2}+\frac{1}{DC^2}+\frac{1}{DD^2}\)
\(\Rightarrow \frac{1}{DK^2}=\frac{1}{a^2}+\frac{1}{a^2}+\frac{1}{a^2}=\frac{3}{a^2}\)
\(\Rightarrow DK=\frac{a\sqrt{3}}{3}\)
Tương tự ta cũng có \(B'H=\frac{a\sqrt{3}}{3}\)
Mà \(B'D=a\sqrt{3}\Rightarrow HK=B'D-B'F-DK\)
\(=a\sqrt{3}-\frac{a\sqrt{3}}{3}- \frac{a\sqrt{3}}{3}=\frac{a\sqrt{3}}{3}\)
Vậy khoảng cách giữa hai mặt phẳng (ACD') và (BA'C') bằng \(HK=\frac{a\sqrt{3}}{3}\).
Câu c:
Vì \(BC'\subset (BA'C')\) bằng \(CD'\subset (BA'C')\), bên cạnh đó (ACD') // (BA'C') suy ra khoảng cách từ BC' đến CD' bằng khoảng cách giữa (ACD') và (BA'C') và bằng \(\frac{a\sqrt{3}}{3}.\)
-- Mod Toán 11 HỌC247
-


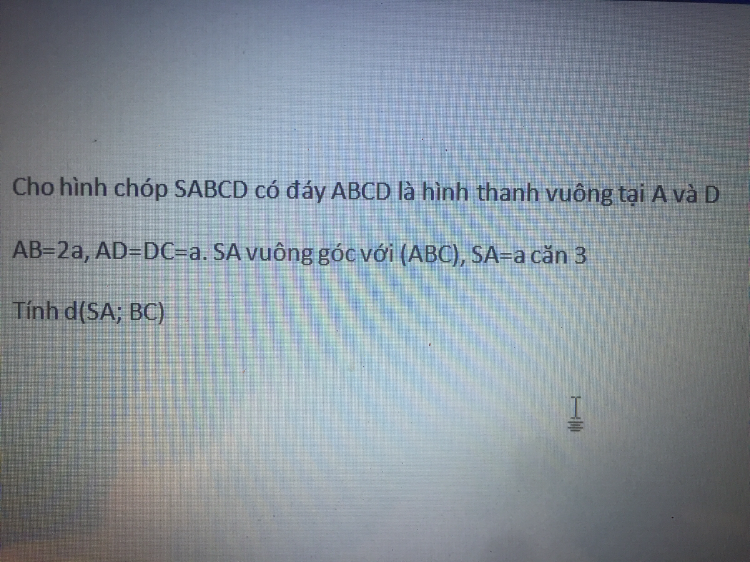
Tính khoảng cách giữa SA và BC.
bởi Trang Minh
 17/07/2020
17/07/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm khoảng cách giữa hai đường thẳng SA và BC?
bởi HiHi
 28/06/2020
28/06/2020
Ai giúp mình câu 32 với ạ
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính theo a khoảng cách từ D đến (SFC)?
bởi minh nguyễn
 28/06/2020
28/06/2020
cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy, gọi I,F lần lượt là trung điểm AB và Ad. Tính theo a khoảng cách từ D đến (SFC)
Theo dõi (1) 7 Trả lời -


Tìm khoảng cách giữa 2 đường chéo nhau?
bởi Hằng Huỳnh Thị Diễm
 27/06/2020
Giúp mình câu 60 với
27/06/2020
Giúp mình câu 60 với Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Câu 26
Câu 26 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 3 trang 119 SGK Hình học 11
Bài tập 4 trang 119 SGK Hình học 11
Bài tập 6 trang 119 SGK Hình học 11
Bài tập 7 trang 119 SGK Hình học 11
Bài tập 8 trang 119 SGK Hình học 11
Bài tập 3.33 trang 160 SBT Hình học 11
Bài tập 3.34 trang 160 SBT Hình học 11
Bài tập 3.35 trang 160 SBT Hình học 11
Bài tập 3.36 trang 160 SBT Hình học 11
Bài tập 3.37 trang 160 SBT Hình học 11
Bài tập 3.38 trang 160 SBT Hình học 11
Bài tập 3.39 trang 160 SBT Hình học 11
Bài tập 3.40 trang 160 SBT Hình học 11
Bài tập 29 trang 117 SGK Hình học 11 NC
Bài tập 30 trang 117 SGK Hình học 11 NC
Bài tập 31 trang 117 SGK Hình học 11 NC
Bài tập 32 trang 117 SGK Hình học 11 NC
Bài tập 33 trang 118 SGK Hình học 11 NC





