Bài tập 31 trang 117 SGK Hình học 11 NC

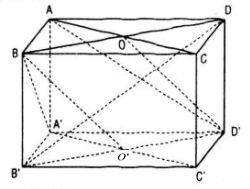
Gọi O, O’ lần lượt là tâm các hình vuông ABCD, A’B’C’D’ của hình lập phương ABCD.A’B’C’D’ cạnh a.

* Ta chứng minh B’D ⊥ (BA’C) và B’D ⊥ (ACD’)

Ta có: 

\(\left\{ \begin{array}{l}
A\prime C\prime  \bot B\prime D\prime \\
A\prime C\prime  \bot BB\prime 
\end{array} \right. \Rightarrow A\prime C\prime  \bot (BB\prime D\prime D)\)

Mà B’D ⊂ (BB’D’D) nên B’D ⊥ A’C’ (1)

Tương tự 

\(\left\{ \begin{array}{l}
AB\prime  \bot A\prime B\\
A\prime B \bot B\prime C\prime 
\end{array} \right. \Rightarrow A\prime B \bot (AB\prime C\prime D)\)

Mà B’D ⊂ (AB’C’D) nên B’D ⊥ A’B (2)

Từ (1) và (2) suy ra B’D ⊥ (BA’C’)

Tương tự ta cũng chứng minh được B’D ⊥ (ACD’)

* Hai mặt phẳng (BA’C’) và (ACD’) song song với nhau, vuông góc với đoạn B’D và chia B’D thành 3 phần bằng nhau (xét hình bình hành BB’DD’ và BO // D’O')

Do đó khoảng cách giữa mp(BA’C) và mp(ACD’) là \(\frac{{B\prime D}}{3} = \frac{{a\sqrt 3 }}{3}\)

* Khoảng cách giữa BC’ và CD’

Khoảng cách giữa hai đường thẳng chéo nhau BC’ và CD’ bằng khoảng cách giữa hai mặt phẳng song song : mp(BA’C’) và mp(ACD’).

Vậy khoảng cách đó là \(\frac{{a\sqrt 3 }}{3}\).

-- Mod Toán 11 HỌC247