Giải bài 3.40 tr 160 SBT Hình học 11
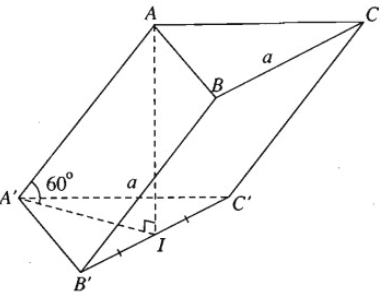
Cho hình lăng trụ tam giác ABC.A'B'C' có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt phẳng đáy góc 60ο và hình chiếu vuông góc của đỉnh A lên mặt phẳng (A'B'C') trùng với trung điểm của cạnh B'C'.
a) Tính khoảng cách giữa hai mặt phẳng đáy của lăng trụ.
b) Chứng minh rằng mặt bên BCC'B' là một hình vuông.
Hướng dẫn giải chi tiết
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và \(\widehat {AA'I} = {60^0}\).
Hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó \(AI = AA'.\sin {60^0} = a.\frac{{\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
b) \(\left. \begin{array}{l}
B'C' \bot A'I\\
B'C' \bot AI
\end{array} \right\} \Rightarrow B'C' \bot \left( {AIA'} \right) \Rightarrow B'C' \bot AA'\)
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.
-- Mod Toán 11 HỌC247
-
Tính d(AN, SD) biết M, N là trung điểm của AB và BC, H là giao của AN và DM
bởi Lâm Canh Nhi
29/04/2018
cho hình chóp s.abcd có abcd là hình vuông cạnh a. M,N lần lượt là trung điểm ab và bc. H là giao điểm của an và dm. sh vuông góc với đáy và sh=a√3. tính
a) d(an;sd)
b)d(cm,sd)
Theo dõi (0) 0 Trả lời -
Tính khoảng cách giữa SC và BD biết chóp S.ABCD có đáy là hình vuông cạnh =1
bởi Yee Trinh
29/04/2018
Cho chóp S.ABCD có đáy là hình vuông cạnh =1 , cạnh SA vuông góc với (ABCD) và SA =1 .Tính khoảng cách giữa SC và BD.
Theo dõi (0) 0 Trả lời -
Tính khoảng cách cách từ A đến (SBD) biết hình chóp SABCD có đáy ABCD là hinh chữ nhật, AB=3, AD=4
bởi Khang Vĩnh
23/04/2018
cho hình chóp SABCD có đáy ABCD là hinh chữ nhật ,AB=3 ,AD=4, SA vuông (ABCD)và SA=5 .
a) tình các khoảng cách từ A đến (SBD)
.b) tính các khoảng cách từ A đến (SBC)
.c)tính các khoảng cách từ O đến (SBC)
Theo dõi (0) 2 Trả lời -
Tính khoảng cách giữa hai đường thẳng SB và AC biết đáy là tam giác vuông cân tại B, BC=a
bởi Nguyễn Lan Anh
19/10/2017
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, BC=a, SA vuông góc với mp(ABC) và SA=2a. tính khoảng cách giữa hai đường thẳng SB và AC
Theo dõi (0) 0 Trả lời -
Tính khoảng cách giữa SD và BC biết M, N, P là trung điểm của SB, SC, SD
bởi Nguyễn Lan Anh
19/10/2017
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt đáy và SA=2a. Gọi M,N,P lần lượt là trung điểm của SB, SC, SD. tính khoảng cách giữa các cặp đường thẳng:
a) SD và BC
b) AD và CM
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 3.38 trang 160 SBT Hình học 11
Bài tập 3.39 trang 160 SBT Hình học 11
Bài tập 29 trang 117 SGK Hình học 11 NC
Bài tập 30 trang 117 SGK Hình học 11 NC
Bài tập 31 trang 117 SGK Hình học 11 NC
Bài tập 32 trang 117 SGK Hình học 11 NC
Bài tập 33 trang 118 SGK Hình học 11 NC
