Giải bài 3.39 tr 160 SBT Hình học 11
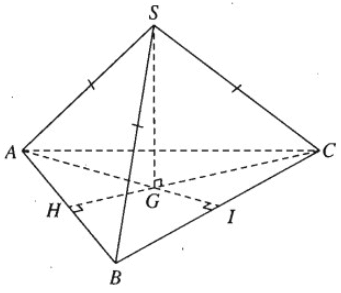
Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC.
a) Tính khoảng cách từ S tới mặt phẳng đáy (ABC).
b) Tính khoảng cách giữa hai đường thẳng AB và SG.
Hướng dẫn giải chi tiết
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có
\(S{G^2} = S{A^2} - A{G^2} = {\left( {2a} \right)^2} - {\left[ {\frac{2}{3}\left( {\frac{{3a\sqrt 3 }}{2}} \right)} \right]^2} = {a^2}\)
Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a
Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó \(HG = \frac{1}{3}HC\) mà \(HC = \frac{{3a\sqrt 3 }}{2}\) nên \(HG = \frac{{a\sqrt 3 }}{2}\).
-- Mod Toán 11 HỌC247
-
Tính khoảng cách từ B đến mp (SAM) biết ABCD là hình bình hành có diện tích 2a^2
bởi Thu Huyền
30/06/2018
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích 2a2, AB = a căn 2,BC=2a. Goi M là trung điểm của CD. Hai mặt phẳng (SBD) và (SAM) cùng vuông góc với đáy. Tính khoảng cách từ đỉnh B đến mặt phẳng (SAM).
Theo dõi (0) 0 Trả lời -
Tính khoảng cách giữa hai mp (MNP) và (ACC') biết hình lăng trụ tứ giác đều ABCD.A'B'C'D'
bởi Thu Huyền
30/06/2018
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a. Gọi M,N,P lần lượt là trung điểm của AD,DC,A'D'. Tính khoảng cách giữa hai mặt phẳng (MNP) và (ACC')
Theo dõi (0) 0 Trả lời -
Tính khoảng cách giữa hai đáy hình lăng trụ ABC.A'B'C' có các cạnh bên hợp với đáy
bởi Thu Huyền
30/06/2018
Cho hình lăng trụ tam giác ABC.A'B'C' có các cạnh bên hợp với đáy những góc bằng 60 độ, đáy ABC là tam giác đều cạnh a và A' cách đều A,B,C. Tính khoảng cách giữa hai đáy hình lăng trụ.
Theo dõi (0) 0 Trả lời -
Tính khoảng cách từ H đến (SAB) biết đáy ABCD là hình chữ nhật tâm I
bởi Nguyễn Thùy Linh
02/06/2018
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật tâm I ,AB=a, BC=a căn 3 , tam giác SAC vuông tại S .Hình chiếu vuông góc của S xuống (ABCD) trùng với trung điểm H của đoạn của đoạn AI. Tính khoảng cách từ H đến (SAB)
Theo dõi (0) 1 Trả lời -
Tính khoảng cách từ B đến mp SCD biết đáy ABCD là hình thang vuông tại A và B
bởi Nguyễn Thùy Linh
01/06/2018
Cho hình chóp SABCD có đáy ABCD là hình thang vuôn tại A và B ,SA=a ,SA vuông góc với ABCD ,AB=BC=a và AD =2a.Khoảng cách từ B đến mặt phẳng SCD tính theo a là ?
Theo dõi (0) 4 Trả lời
Bài tập SGK khác
Bài tập 3.37 trang 160 SBT Hình học 11
Bài tập 3.38 trang 160 SBT Hình học 11
Bài tập 3.40 trang 160 SBT Hình học 11
Bài tập 29 trang 117 SGK Hình học 11 NC
Bài tập 30 trang 117 SGK Hình học 11 NC
Bài tập 31 trang 117 SGK Hình học 11 NC
Bài tập 32 trang 117 SGK Hình học 11 NC
Bài tập 33 trang 118 SGK Hình học 11 NC
