HOC247 mß╗Øi c├Īc em hß╗Źc sinh tham khß║Żo b├Āi Tam gi├Īc bß║▒ng nhau To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo b├¬n dŲ░ß╗øi ─æ├óy, th├┤ng qua b├Āi giß║Żng n├Āy c├Īc em dß╗ģ d├Āng hß╗ć thß╗æng lß║Īi to├Ān bß╗Ö kiß║┐n thß╗®c ─æ├Ż hß╗Źc, b├¬n cß║Īnh ─æ├│ c├Īc em c├▓n nß║»m ─æŲ░ß╗Żc phŲ░ŲĪng ph├Īp giß║Żi c├Īc b├Āi tß║Łp v├Ā vß║Łn dß╗źng v├Āo giß║Żi c├Īc b├Āi tß║Łp tŲ░ŲĪng tß╗▒. Ch├║c c├Īc em c├│ mß╗Öt tiß║┐t hß╗Źc thß║Łt hay v├Ā thß║Łt vui khi ─æß║┐n lß╗øp!
T├│m tß║»t l├Į thuyß║┐t
1.1. Hai tam gi├Īc bß║▒ng nhau
|
Hai tam gi├Īc bß║▒ng nhau l├Ā hai tam gi├Īc c├│ c├Īc cß║Īnh tŲ░ŲĪng ß╗®ng bß║▒ng nhau, c├Īc g├│c tŲ░ŲĪng ß╗®ng bß║▒ng nhau. |
|---|
Ch├║ ├Į: Khi vß║Į h├¼nh hai tam gi├Īc bß║▒ng nhau, c├Īc cß║Īnh hoß║Ęc c├Īc g├│c bß║▒ng nhau ─æŲ░ß╗Żc ─æ├Īnh dß║źu bß╗¤i nhß╗»ng k├Ł hiß╗ću giß╗Śng nhau (H├¼nh b├¬n dŲ░ß╗øi)
V├Ł dß╗ź: Quan s├Īt H├¼nh b├¬n dŲ░ß╗øi, cho biß║┐t hai tam gi├Īc ABC v├Ā MIN c├│ bß║▒ng nhau kh├┤ng. Chß╗ē ra c├Īc cß║Ęp g├│c v├Ā c├Īc cß║Ęp cß║Īnh tŲ░ŲĪng ß╗®ng bß║▒ng nhau.
Giß║Żi
Hai tam gi├Īc ABC v├Ā MIN b─āng nhau v├¼ c├│ c├Īc cß║Īnh tŲ░ŲĪng ß╗®ng b─āng nhau, c├Īc g├│c tŲ░ŲĪng ß╗®ng b─āng nhau.
C├Īc cß║Ęp g├│c tŲ░ŲĪng ß╗®ng b─āng nhau l├Ā: \(\widehat A = \widehat I;\widehat C = \widehat N;\widehat B = \widehat M\left( { = {{180}^0} - {{80}^0} - {{30}^0} = {{70}^0}} \right)\).
C├Īc cß║Ęp cß║Īnh tŲ░ŲĪng ß╗®ng bß║▒ng nhau l├Ā: AB = IM; AC = IN; BC=MN.
1.2. C├Īc trŲ░ß╗Øng hß╗Żp bß║▒ng nhau cß╗¦a hai tam gi├Īc
a) TrŲ░ß╗Øng hß╗Żp bß║▒ng nhau thß╗® nhß║źt: Cß║Īnh - cß║Īnh - cß║Īnh (c.c.c)
|
Nß║┐u ba cß║Īnh cß╗¦a lam gi├Īc n├Āy bß║▒ng ba cß║Īnh cß╗¦a tam gi├Īc kia th├¼ hai tam gi├Īc ─æ├│ bß║▒ng nhau. |
|---|
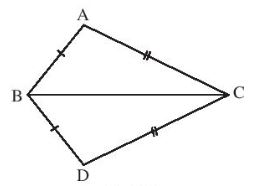
V├Ł dß╗ź: Trong H├¼nh sau, chß╗®ng minh rß║▒ng \(\Delta ABC = \Delta DBC\).
Giß║Żi
X├®t \(\Delta ABC\) v├Ā \(\Delta DBC\), ta c├│:
BC l├Ā cß║Īnh chung;
BA = BD;
CA = CD.
Suy ra \(\Delta ABC = \Delta DBC\) (c.c.c)
b) TrŲ░ß╗Øng hß╗Żp bß║▒ng nhau thß╗® hai: Cß║Īnh - g├│c - cß║Īnh (c.g.c)
|
Nß║┐u hai cß║Īnh v├Ā g├│c xen giß╗»a cß╗¦a tam gi├Īc n├Āy bß║▒ng hai cß║Īnh v├Ā g├│c xen giß╗»a cß╗¦a tam gi├Īc kia th├¼ hai tam gi├Īc ─æ├│ bß║▒ng nhau. |
|---|
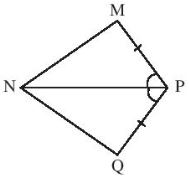
V├Ł dß╗ź: Trong h├¼nh sau, Chß╗®ng minh rß║▒ng \(\Delta MNP = \Delta QNP\).
Giß║Żi
X├®t \(\Delta MNP\) v├Ā \(\Delta QNP\), ta c├│:
PN l├Ā cß║Īnh chung;
\(\widehat {MNP} = \widehat {QPN}\);
PM = PQ.
Suy ra: \(\Delta MNP = \Delta QNP\) (c.g.c).
c) TrŲ░ß╗Øng hß╗Żp bß║▒ng nhau thß╗® ba: g├│c - cß║Īnh - g├│c (g.c.g)
|
Nß║┐u mß╗Öt cß║Īnh v├Ā hai g├│c kß╗ü cß╗¦a tam gi├Īc n├Āy bß║▒ng mß╗Öt cß║Īnh v├Ā hai g├│c kß╗ü cß╗¦a tam gi├Īc kia th├¼ hai tam gi├Īc ─æß╗Å bß║▒ng nhau. |
|---|
V├Ł dß╗ź: Trong H├¼nh sau, chß╗®ng mß╗ēnh rß║▒ng \(\Delta EFG = \Delta HGF\).
Giß║Żi
X├®t \(\Delta EFG\) v├Ā \(\Delta HGF\), ta c├│:
\(\widehat {EFG} = \widehat {HGF}\);
GF l├Ā cß║Īnh chung;
\(\widehat {EGF} = \widehat {HFG}\);
Suy ra \(\Delta EFG = \Delta HGF\) (g.c.g)
1.3. C├Īc trŲ░ß╗Øng hß╗Żp bß║▒ng nhau cß╗¦a hai tam gi├Īc vu├┤ng
TrŲ░ß╗Øng hß╗Żp hai cß║Īnh g├│c vu├┤ng
|
Nß║┐u hai cß║Īnh g├│c vu├┤ng cß╗¦a tam gi├Īc vu├┤ng n├Āy lß║¦n lŲ░ß╗Żt bß║▒ng hai cß║Īnh g├│c vu├┤ng cß╗¦a tam gi├Īc vu├┤ng kia th├¼ hai tam gi├Īc vu├┤ng ─æ├│ b─āng nhau (theo trŲ░ß╗Øng hß╗Żp c.g.c). |
|---|
TrŲ░ß╗Øng hß╗Żp mß╗Öt cß║Īnh g├│c vu├┤ng v├Ā mß╗Öt g├│c nhß╗Źn kß╗ü cß║Īnh ß║źy
|
Nß║┐u mß╗Öt cß║Īnh g├│c vu├┤ng v├Ā mß╗Öt g├│c nhß╗Źn kß╗ü cß║Īnh ß║źy cß╗¦a ta gi├Īc vu├┤ng n├Āy bß║▒ng mß╗Öt cß║Īnh g├│c vu├┤ng v├Ā mß╗Öt g├│c nhß╗Źn kß╗ü cß║Īnh ß║źy cß╗¦a tam gi├Īc vu├┤ng kia th├¼ hai tam gi├Īc vu├┤ng ─æ├│ bß║▒ng nhau (theo trŲ░ß╗Øng hß╗Żp g.c.g). |
|---|
TrŲ░ß╗Øng hß╗Żp cß║Īnh huyß╗ģn v├Ā mß╗Öt g├│c nhß╗Źn
|
Nß║┐u cß║Īnh huyß╗ün v├Ā mß╗Öt g├│c nhß╗Źn cß╗¦a tam gi├Īc vu├┤ng n├Āy bß║▒ng cß║Īnh huyß╗ün v├Ā mß╗Öt g├│c nhß╗Źn cß╗¦a tam gi├Īc vu├┤ng kia thi hai tam gi├Īc vu├┤ng ─æß╗Å b─āng nhau (theo trŲ░ß╗Øng hß╗Żp g.c.g). |
|---|
V├Ł dß╗ź: H├Ży chß╗ē ra c├Īc cß║Ęp tam gi├Īc bß║▒ng nhau trong h├¼nh dŲ░ß╗øi ─æ├óy v├Ā cho biß║┐t ch├║ng bß║▒ng nhau theo trŲ░ß╗Øng hß╗Żp n├Āo cß╗¦a tam gi├Īc vu├┤ng.
Giß║Żi
a) X├®t \(\Delta\)AHB v├Ā \(\Delta\)AHC c├╣ng vu├┤ng tß║Īi H, ta c├│:
AH l├Ā cß║Īnh chung;
HB = HC.
Suy ra \(\Delta\)AHB = \(\Delta\)AHC theo trŲ░ß╗Øng hß╗Żp hai cß║Īnh g├│c vu├┤ng.
b) X├®t \(\Delta\)DKE v├Ā \(\Delta\)DKF c├╣ng vu├┤ng tß║Īi K, ta c├│:
DK l├Ā cß║Īnh chung;
\(\widehat {EDK} = \widehat {FDK}\).
Suy ra \(\Delta\)DKE = \(\Delta\)DKF theo trŲ░ß╗Øng hß╗Żp mß╗Öt cß║Īnh g├│c vu├┤ng v├Ā mß╗Öt g├│c nhß╗Źn kß╗ü cß║Īnh ß║źy.
c) X├®t \(\Delta\)MNP vu├┤ng tß║Īi M v├Ā \(\Delta\) QNP vu├┤ng tß║Īi Q, ta c├│:
NP l├Ā cß║Īnh huyß╗ün chung;
\(\widehat {MPN} = \widehat {QPN}\).
Suy ra \(\Delta\)MNP = \(\Delta\) QNP theo trŲ░ß╗Øng hß╗Żp cß║Īnh huyß╗ün v├Ā mß╗Öt g├│c nhß╗Źn.
B├Āi tß║Łp minh hß╗Źa
C├óu 1: Trong H├¼nh 5, cho biß║┐t. H├Ży t├Łnh sß╗æ ─æo g├│c M v├Ā ─æß╗Ö d├Āi cß║Īnh GI.
HŲ░ß╗øng dß║½n giß║Żi
Theo ─æß╗ŗnh l├Ł tß╗Ģng 3 g├│c trong tam gi├Īc ta c├│ :
\(\widehat G + \widehat H + \widehat I = {180^o} \Rightarrow \widehat G = {180^o} - {62^o} - {43^o} = {75^o}\)
M├Ā \(\widehat G = \widehat M\) ( g├│c tŲ░ŲĪng ß╗®ng trong 2 tam gi├Īc bß║▒ng nhau )
\( \Rightarrow \widehat M = {75^o}\)
C├óu 2: Cho \(\widehat {xOy}\). Vß║Į cung tr├▓n t├óm O, cung n├Āy cß║»t Ox, Oy theo thß╗® tß╗▒ tß║Īi M, N. Vß║Į hai cung tr├▓n t├óm M v├Ā t├óm N c├│ c├╣ng b├Īn k├Łnh sao cho ch├║ng cß║»t nhau tß║Īi ─æiß╗ām P nß║▒m trong \(\widehat {xOy}\). Nß╗æi O vß╗øi P (H├¼nh 16). H├Ży chß╗®ng minh rß║▒ng , tß╗½ ─æ├│ suy ra OP l├Ā tia ph├ón gi├Īc cß╗¦a \(\widehat {xOy}\).
HŲ░ß╗øng dß║½n giß║Żi
V├¼ M, N thuß╗Öc ─æŲ░ß╗Øng tr├▓n t├óm O c├│ c├╣ng b├Īn k├Łnh n├¬n OM = ON = b├Īn k├Łnh cung tr├▓n t├óm O
Tß╗½ M, N vß║Į 2 cung tr├▓n c├│ c├╣ng b├Īn k├Łnh v├Ā 2 ─æŲ░ß╗Øng tr├▓n cß║»t nhau tß║Īi P
Suy ra P thuß╗Öc cß║Ż 2 cung tr├▓n t├óm M, N c├│ c├╣ng b├Īn k├Łnh n├¬n MP = NP
X├®t tam gi├Īc OMP v├Ā tam gi├Īc ONP ta c├│ :
OM = ON
OP cß║Īnh chung
MP = NP
\(\Rightarrow \Delta{OMP}=\Delta{ONP}\) ( c-c-c )
\( \Rightarrow \widehat {MOP} = \widehat {PON}\) (2 g├│c tŲ░ŲĪng ß╗®ng)
Do ─æ├│, OP l├Ā ph├ón gi├Īc \(\widehat {xOy}\)
Luyß╗ćn tß║Łp ChŲ░ŲĪng 8 B├Āi 2 To├Īn 7 CTST
Qua b├Āi giß║Żng ß╗¤ tr├¬n, gi├║p c├Īc em hß╗Źc sinh:
- Nhß║Łn biß║┐t ─æŲ░ß╗Żc kh├Īi niß╗ćm hai tam gi├Īc bß║▒ng nhau.
- Giß║Żi th├Łch ─æŲ░ß╗Żc c├Īc trŲ░ß╗Øng hß╗Żp bß║▒ng nhau cß╗¦a hai tam gi├Īc.
- Giß║Żi th├Łch ─æŲ░ß╗Żc c├Īc trŲ░ß╗Øng hß╗Żp bß║▒ng nhau cß╗¦a hai tam gi├Īc vu├┤ng.
3.1. B├Āi tß║Łp trß║»c nghiß╗ćm ChŲ░ŲĪng 8 B├Āi 2 To├Īn 7 CTST
─Éß╗ā cß╗¦ng cß╗æ b├Āi hß╗Źc xin mß╗Øi c├Īc em c├╣ng l├Ām B├Āi kiß╗ām tra Trß║»c nghiß╗ćm To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo ChŲ░ŲĪng 8 B├Āi 2 ─æß╗ā kiß╗ām tra xem m├¼nh ─æ├Ż nß║»m ─æŲ░ß╗Żc nß╗Öi dung b├Āi hß╗Źc hay chŲ░a.
C├óu 4-10: Mß╗Øi c├Īc em ─æ─āng nhß║Łp xem tiß║┐p nß╗Öi dung v├Ā thi thß╗Ł Online ─æß╗ā cß╗¦ng cß╗æ kiß║┐n thß╗®c v├Ā nß║»m vß╗»ng hŲĪn vß╗ü b├Āi hß╗Źc n├Āy nh├®!
3.2. B├Āi tß║Łp SGK ChŲ░ŲĪng 8 B├Āi 2 To├Īn 7 CTST
B├¬n cß║Īnh ─æ├│ c├Īc em c├│ thß╗ā xem phß║¦n hŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo ChŲ░ŲĪng 8 B├Āi 2 ─æß╗ā gi├║p c├Īc em nß║»m vß╗»ng b├Āi hß╗Źc v├Ā c├Īc phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp.
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 1 trang 48 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Thß╗▒c h├Ānh 1 trang 49 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Vß║Łn dß╗źng 1 trang 49 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 2 trang 50 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 3 trang 51 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 4 trang 52 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Thß╗▒c h├Ānh 2 trang 54 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Thß╗▒c h├Ānh 3 trang 54 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Vß║Łn dß╗źng 2 trang 54 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Vß║Łn dß╗źng 3 trang 54 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 5 trang 55 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Thß╗▒c h├Ānh 4 trang 56 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 6 trang 56 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Thß╗▒c h├Ānh 5 trang 57 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 1 trang 57 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 2 trang 57 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 3 trang 58 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 4 trang 58 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 5 trang 58 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 6 trang 58 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 7 trang 58 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 8 trang 58 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 9 trang 58 SGK To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 1 trang 45 SBT To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 2 trang 45 SBT To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 3 trang 45 SBT To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 4 trang 45 SBT To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 5 trang 46 SBT To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 6 trang 46 SBT To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 7 trang 46 SBT To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 8 trang 46 SBT To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi b├Āi 9 trang 46 SBT To├Īn 7 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Hß╗Åi ─æ├Īp ChŲ░ŲĪng 8 B├Āi 2 To├Īn 7 CTST
Trong qu├Ī tr├¼nh hß╗Źc tß║Łp nß║┐u c├│ thß║»c mß║»c hay cß║¦n trß╗Ż gi├║p g├¼ th├¼ c├Īc em h├Ży comment ß╗¤ mß╗źc Hß╗Åi ─æ├Īp, Cß╗Öng ─æß╗ōng To├Īn HOC247 sß║Į hß╗Ś trß╗Ż cho c├Īc em mß╗Öt c├Īch nhanh ch├│ng!
Ch├║c c├Īc em hß╗Źc tß║Łp tß╗æt v├Ā lu├┤n ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp!
-- Mod To├Īn Hß╗Źc 7 Hß╗īC247


.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)





