Giải bài 9 trang 46 SBT Toán 7 Chân trời sáng tạo tập 2
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OA = OC, OB = OD. Gọi M là giao điểm của AD và CB. Chứng minh rằng:
a) AD = CB
b) \(\Delta MAB = \Delta MC{\rm{D}}\)
Hướng dẫn giải chi tiết Bài 9
Phương pháp giải
- Chứng minh hai tam giác chưa hai cạnh tương ứng bằng nhau.
- Xét các điều kiện của hai tam giác MAB và MCD xem hai tam đó bằng nhau theo trường hợp nào?
Lời giải chi tiết
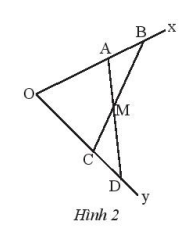
a) Xét tam giác AOD và tam giác COB có:
OA = OC
\(\widehat O\) chung
OB = OD
Suy ra: \(\Delta AO{\rm{D}} = \Delta COB(c - g - c)\)
b) Ta có: \(\Delta AO{\rm{D}} = \Delta COB(c - g - c)\)(chứng minh trên)
Xét tam giác MAB và tam giác MCD có:
Do đó: \(\widehat {MBA} = \widehat {M{\rm{D}}C};\widehat {MAB} = \widehat {MC{\rm{D}}}\) (cùng bù hai góc bằng nhau)
AB = CD (vì OA = OC, OB = OD)
Suy ra: \(\Delta MAB = \Delta MC{\rm{D(g - c - g)}}\)
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





