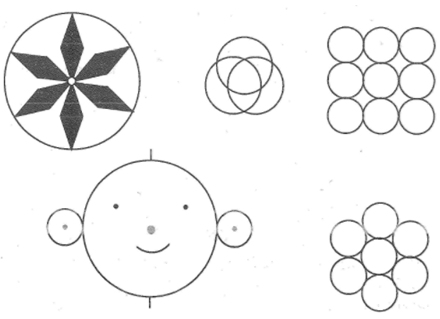
Bài tập 39 trang 93 SBT Toán 6 Tập 2
Vẽ lại các hình sau (cho đúng kích thước như hình đã cho).
Hướng dẫn giải chi tiết
Sử dụng các dụng cụ để vẽ lại các hình như trên
-- Mod Toán 6 HỌC247
-


Chứng minh tứ giác ABOC là hình thoi
bởi Huong Duong
 21/01/2019
21/01/2019
Cho đường tròn (O) có bán kính OA = R, dây BC vuông góc với OA tại trung điểm I của OA.
a, CM: Tứ giác ABOC là hình thoi
b, Tính BC theo R.
c, Kẻ đường kính C. CM: BE // OA.
d, Kẻ trung tuyến với tâm O tại B, nó cắt đường thẳng OA tại D:
BD=?CM: BD là trung tuyến tâm OTheo dõi (0) 1 Trả lời -


Chứng minh MA=MT
bởi thi trang
 22/01/2019
22/01/2019
Cho AB,AC là 2 tiếp điểm của (O).Gọi E,F lần lượt là trung điểm của AB,AC.Trên EF lấy 1 điểm M bất kỳ,từ M kẽ tiếp tuyến MT với (O).
Chứng Minh: MA=MT
(Ai giải được,vẽ hình cụ thể được 2GP)( @phynit)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng A,E,F thẳng hàng
bởi Hoàng My
 22/01/2019
22/01/2019
Chi đường tròn O và đường kính AB cố định. Gọi M là điểm di động trên đường tròn O sao cho M ko trùng với A và B. Đường thẳng vuông goc với AB tại C cắt đường thẳng M tại N. Đường thẳng BN cắt đường tròn tại E. Các đường thăngt BM và CN cắt nhau tại F. Chứng minh rằng:
a) A,E,F thẳng hàng.
b) AM.AN không đổi.
c) A là trọng tâm của tam giác BNF và chỉ khi NF ngắn nhất.
Theo dõi (0) 1 Trả lời -


Chứng minh AD^2=BM.DN
bởi thu trang
 22/01/2019
22/01/2019
Cho hình thoi ABCD có góc A=60 độ .M là một điểm trên BC,đường thẳng MA cắt cạnh DC kéo dài tại N.
1)Chứng minh: AD2=BM.DN
2)Đường thẳng DM cắt BN tại E.Chứng minh rằng tứ giác BECD là tứ giác nội tiếp.
3)Khi hình thoi ABCD cố định.Chứng minh rằng điểm E nằm trên 1 đường tròn khi M thay đổi trên cạnh BC.Theo dõi (0) 1 Trả lời -


Xác định m để phương trình 8x^3+8x+m^2+1=0 có 2 nghiệm x_1, x_2 thoã mãn x_1^4-x_2^4=x_1^3-x_2^3
bởi Lê Thánh Tông
 22/01/2019
22/01/2019
Cho pt:\(8x^{2\:\:\:}\)-8x+\(^{m2}\)+1=0
Xác định m để pt có 2 no x1,x2 thoã mãn:x1^4-x2^4=x1^3-x2^3
Theo dõi (0) 1 Trả lời -


Chứng minh AEDO nội tiếp
bởi Trịnh Lan Trinh
 22/01/2019
22/01/2019
Cho hình thang cân ABCD (AB>CD) nội tiếp đường tròn (O). Kẻ các tiếp tuyến của (O) tại A và D chúng cắt nhau tại E. Gọi M là giao điểm của hai đường chéo AC và BD
a) Chứng minh: AEDO nội tiếp
b) AB//EM
c) EM giao cạnh bên AD và BC của hình thang lần lượt tại H và K. Chứng minh: M là trung điểm của HK
d) Chứng minh: \(\dfrac{2}{HK}=\dfrac{1}{AB}+\dfrac{1}{CD}\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng BD là tiếp tuyến của (C)
bởi Nguyễn Trà Long
 22/01/2019
22/01/2019
Cho tam giác ABC có \(\widehat{ABC}\) =90 (AB>AC). Đường cao AH cắt (C;CA) tại D
a. CMR BD là tiếp tuyến của (C)
b. Qua C kẻ đường vuông góc với BC cắt 2 tia BA,BD theo thứ tự tại E,F. Trên cung nhỏ AD của (C) lấy M bất kì. Qua M kẻ tiếp tuyến với C cắt AB,BD lần lượt tại P,Q.CMR 2\(\sqrt{PE.QF}\)=EF
Ai giúp mình câu b với
Theo dõi (0) 1 Trả lời -


Chứng minh OA vuông góc với BC và DC // OA
bởi Nguyễn Minh Minh
 22/01/2019
22/01/2019
Cho đường tròn ( O ; R ), điểm A nằm ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn ( B, C là các tiếp điểm). Kẻ đường kính BD. Chứng minh : OA vuông góc với BC và DC // OA.
(Giúp mình với nhé :v mai kiểm tra rồi :v)
Theo dõi (0) 1 Trả lời -


Cho ba đường tròn bằng nhau, bán kính là 5cm. Tính diện tích phần được tô màu.
Theo dõi (0) 1 Trả lời -


Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn. Từ A vẽ các tiếp tuyến AB, AC của (O;R), (BC là các tiếp điểm).
1) Chứng minh rằng bốn điểm A,B,O,C cùng thuộc một đường tròn;
2) Lấy điểm I trên đường tròn (O;R) sao cho tia OI nằm giữa hai tia OA và OB. Qua I vẽ đường thẳng tiếp xúc với đường tròn (O;R) cắt AB,AC lần lượt tại M và N. Chứng minh MB+NC=MN;
3) Qua O vẽ đường thẳng vuông góc với OA cắt AB,AC lần lượt tại P và Q. Chứng minh rằng PM.QN=\(\dfrac{PQ^2}{4}\)
Theo dõi (0) 1 Trả lời -


Cho ΔABC. Qua A vẽ (d) cắt BC tại D.
Tìm vị trí của điểm D để tổng khoảng cách từ B và C đến (d) nhỏ nhất
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác ABOC nội tiếp
bởi Co Nan
 22/01/2019
22/01/2019
Bài 5: Cho đường tròn (O;R) và một điểm A nằm ngoài đường tròn . Từ A kẻ tiếp tuyến AB và AC với đường tròn. trên cung nhỏ BC lấy điểm I, qua I vẽ tiếp tuyến với đường tròn cắt AB và AC lần lượt tại M và N. Nối B và C cắt OM và ON lần lượt tại H và K.
a. chứng ming tứ giác ABOC nội tiếp
b. chứng minh: BM + CN= MN
c. chứng minh: góc MON = \(\dfrac{1}{2}\) góc BOC
d. chứng minh: OI MK, NH đồng quyTheo dõi (0) 1 Trả lời -


Chứng minh tứ giác BCRF nội tiếp
bởi Bo bo
 22/01/2019
22/01/2019
Cho tam giác ABC nhọn. Đường tròn tâm O đường kính AB và đường tròn tâm O' đường kính AC cát AC, AB lần lượt ở E, F. Gọi M,N lần lượt là giao điểm của đoạn thẳng CF, BE với (O) và (O').
Chứng minh:
a. Tứ giác BCRF nội tiếp.
b. tam giác AMN cân.giúp mình câu b với ạ
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 38 trang 91 SGK Toán 6 Tập 2
Bài tập 39 trang 92 SGK Toán 6 Tập 2
Bài tập 40 trang 92 SGK Toán 6 Tập 2
Bài tập 41 trang 92 SGK Toán 6 Tập 2
Bài tập 42 trang 93 SGK Toán 6 Tập 2
Bài tập 35 trang 93SBT Toán 6 Tập 2
Bài tập 36 trang 93 SBT Toán 6 Tập 2
Bài tập 37 trang 93 SBT Toán 6 Tập 2
Bài tập 38 trang 93 SBT Toán 6 Tập 2
Bài tập 8.1 trang 94 SBT Toán 6 Tập 2